En este post te explicamos qué son las ecuaciones bicuadradas y cómo se resuelven. Además, hemos resuelto paso a paso varios ejercicios de ecuaciones bicuadradas para que puedas practicar.
Índice
¿Qué son las ecuaciones bicuadradas?
Las ecuaciones bicuadradas son ecuaciones de cuarto grado que solamente tienen términos de grado par, es decir, las ecuaciones bicuadradas son de la forma ax4+bx2+c=0.
Fíjate que la expresión algebraica de una ecuación bicuadrada es como la de una ecuación de segundo grado completa pero con sus exponentes multiplicados por 2. Más abajo veremos por qué es importante esta relación.
Cómo resolver las ecuaciones bicuadradas
Los pasos que se deben hacer para resolver las ecuaciones bicuadradas son:
- Hacer un cambio de variable (x2=t), para transformar la ecuación bicuadrada en una ecuación de segundo grado.
- Resolver la ecuación de segundo grado hallada en el paso anterior con la fórmula general.
- Deshacer el cambio de variable y obtener las soluciones de la ecuación bicuadrada.
Este es el procedimiento que nos permitirá hacer cualquier tipo de ecuación bicuadrada, sin embargo, seguro que lo entiendes mejor con un ejemplo explicado paso a paso.
Ejemplo de una ecuación bicuadrada resuelta
Así pues, para que veas exactamente cómo se solucionan las ecuaciones bicuadradas, a continuación vamos a explicar la resolución de un ejemplo paso a paso:
Lo primero que debemos hacer para resolver la ecuación bicuadrada es aplicar el cambio de variable x2=t. De este modo, transformamos la ecuación bicuadrada en una ecuación cuadrática, porque el exponente de grado 4 pasa a ser de grado 2, y el exponente de grado 2 se convierte en grado 1:
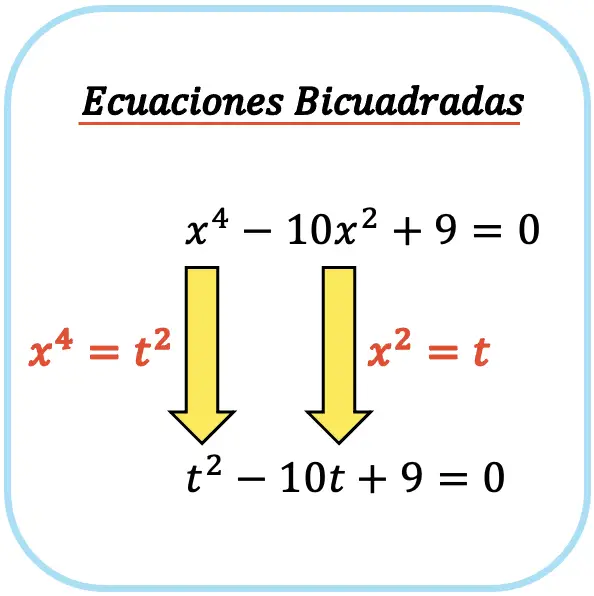
De esta forma hemos podido convertir la ecuación bicuadrada en una ecuación de segundo grado completa, que ya sabemos cómo resolverla.
Por lo tanto, aplicamos la fórmula general de las ecuaciones de segundo grado para solucionar la ecuación obtenida:
Una vez hemos calculado los valores de la variable t, debemos deshacer el cambio de variable para hallar los valores de la incógnita x. Para ello, simplemente tenemos que hacer la raíz cuadrada de cada valor obtenido en el paso anterior:
- Si t = 9:
- Si t = 1:
Por lo tanto las cuatro soluciones de la ecuación bicuadrada son:
Ejercicios resueltos de las ecuaciones bicuadradas
A continuación, hemos resuelto varios ejercicios de ecuaciones bicuadradas para que puedas practicar. Ten en cuenta que están ordenados por dificultad, por lo que las primeras ecuaciones bicuadradas son las más fáciles y las últimas ecuaciones bicuadradas son las más difíciles. Recuerda también que puedes dejarnos cualquier duda que tengas en los comentarios.⬇⬇⬇
Ejercicio 1
Resuelve la siguiente ecuación bicuadrada:
Efectivamente, se trata de una ecuación bicuadrada porque solo tiene término de cuarto grado, término de segundo grado, y término independiente.
En primer lugar, tenemos que hacer el cambio de variable x2=t y x4=t2 para transformar la ecuación bicuadrada en una ecuación cuadrática:
Entonces utilizamos la fórmula general de las ecuaciones cuadráticas para resolver la ecuación resultante:
Y, finalmente, deshacemos el cambio de variable para hallar los valores de la incógnita x. Para ello, tenemos que calcular la raíz cuadrada de cada valor obtenido en el paso anterior:
Si t = 4:
Si t = 1:
En definitiva, las cuatro soluciones de la ecuación bicuadrada son:
Ejercicio 2
Calcula la siguiente ecuación bicuadrada:
La ecuación es bicuadrada ya que no tiene ningún término de grado impar, así que debemos utilizar el método explicado más arriba.
Primero hacemos el cambio de variable x2=t y x4=t2 para convertir la ecuación bicuadrada en una ecuación de segundo grado:
Ahora aplicamos la fórmula general de las ecuaciones de segundo grado para resolverla:
Y, por último, deshacemos el cambio de variable para hallar los valores de la incógnita x:
Si t = 25:
Si t = 4:
En conclusión, las 4 soluciones de la ecuación bicuadrada son:
Ejercicio 3
Soluciona la siguiente ecuación bicuadrada:
La ecuación es del tipo bicuadrada porque todos sus exponentes son pares, por lo tanto, hacemos el cambio de variable x2=t y x4=t2 para reducir los exponentes de la ecuación:
Usamos la fórmula general de las ecuaciones de segundo grado para solucionar la ecuación conseguida:
Entonces, para encontrar las soluciones de la ecuación bicuadrada, deshacemos el cambio de variable y efectuamos la raíz cuadrada:
Si t = 36:
Si t = 16:
Así que la ecuación bicuadrada tiene por soluciones los siguientes valores:
Ejercicio 4
Resuelve la siguiente ecuación de cuarto grado:
Aunque no tenga término de grado cero, consiste en una ecuación bicuadrada porque todos sus exponentes son pares. De manera que hacemos el cambio de variable x2=t y x4=t2 para convertirla en una ecuación de segundo grado:
En este problema no hace falta emplear la fórmula general, ya que se trata de una ecuación de segundo grado incompleta. En consecuencia, debemos sacar factor común:
Igualamos cada factor del producto anterior a 0 y resolvemos las dos ecuaciones de primer grado resultantes:
Y, para terminar, deshacemos el cambio de variable y calculamos la raíz cuadrada de los dos valores obtenidos en el paso anterior:
Si t = 0:
Si t = 16:
Así que la ecuación bicuadrada tiene 3 soluciones, y una de ellas (x=0) es solución doble:
Ejercicio 5
Determina las soluciones de la siguiente ecuación bicuadrada:
Para resolver la ecuación bicuadrada tenemos que aplicar el cambio de variable x2=t y x4=t2 para convertirla en una ecuación de grado 2:
Ahora aplicamos la fórmula general de las ecuaciones de segundo grado para resolverla:
En este problema hemos obtenido una única solución de la ecuación cuadrática, por lo que solo deshacemos el cambio de variable una sola vez:
Si t = 4:
En conclusión, la ecuación bicuadrada solo tiene 2 soluciones, pero ambas son soluciones dobles ya que una ecuación de grado 4 necesita 4 soluciones:
Ejercicio 6
Resuelve la siguiente ecuación de grado 4:
La ecuación es del tipo bicuadrada debido a que todas las incógnitas están elevadas a exponentes pares, por tanto, hacemos el cambio de variable x2=t y x4=t2 para transformarla en una ecuación de segundo grado:
En segundo lugar, usamos la fórmula general de las ecuaciones de segundo grado para solucionarla:
Finalmente, para hallar las soluciones de la ecuación bicuadrada, deshacemos el cambio de variable y calculamos la raíz cuadrada de los valores encontrados:
Si t = 81:
Si t = -1:
No existen las raíces cuadradas de números negativos.
Por lo tanto, la ecuación bicuadrada solo tiene dos soluciones reales
En realidad, también se podrían encontrar dos soluciones a partir de la raíz de -1, pero entonces sería una ecuación bicuadrada con soluciones complejas y para entender este concepto se necesita un nivel de matemáticas más avanzado.
Ejercicio 7
Resuelve la siguiente ecuación bicuadrada con fracciones:
Antes de aplicar el método para resolver ecuaciones bicuadradas, quitaremos las fracciones de la ecuación para simplificar los cálculos. Para ello, multiplicamos cada término de la ecuación por el mínimo común múltiplo de los denominadores, que es 12:
Y quitamos las fracciones dividiendo el 12 entre cada denominador:
Ahora así, hacemos el cambio de variable x2=t y x4=t2 para transformar algebraicamente la ecuación:
Aplicamos la fórmula general de las ecuaciones cuadráticas:
Para averiguar las soluciones de la ecuación bicuadrada, deshacemos el cambio de variable y realizamos la raíz cuadrada de cada valor hallado en el paso anterior:
Si t = 8:
Si t = 2:
Así que la ecuación bicuadrada tiene 4 soluciones radicales:
Ejercicio 8
Resuelve la siguiente ecuación con el método de las ecuaciones bicuadradas:
En este ejercicio la ecuación no es bicuadrada porque tiene un término cúbico, sino que se trata de una ecuación bicúbica (o tricuadrada). Sin embargo, este tipo de ecuaciones se pueden resolver de la misma manera que las ecuaciones bicuadradas, la diferencia es que el cambio de variable debe ser x3=t y x6=t2 para así transformar la ecuación bicúbica en una ecuación de segundo grado:
Ahora aplicamos la fórmula general de las ecuaciones cuadráticas para resolver la ecuación resultante:
Y, finalmente, deshacemos el cambio de variable para hallar los valores de la incógnita x. Pero en este caso tenemos que hacer la raíz cúbica en lugar de la raíz cuadrada:
Si t = 27:
Si t = -8:
Las raíces cúbicas de números reales negativos sí que existen.
En conclusión, la ecuación bicúbica tiene 2 soluciones reales:

muy bueno bastante claro
¡Gracias Máximo!