En este post veremos qué es la programación lineal y cómo resolver problemas mediante la programación lineal. Además, encontrarás varios ejercicios resueltos paso a paso de programación lineal para poder practicar.
Para poder entender de qué se trata la programación lineal, previamente tienes que dominar las inecuaciones. Así que antes de seguir te recomendamos que primero le eches un vistazo a cómo resolver una inecuación.
Índice
¿Qué es la programación lineal?
La programación lineal, también llamada programa lineal, es un método que optimiza (maximiza o minimiza) una función lineal de más de una variable que está sujeta a varias restricciones. Estás restricciones suelen ser inecuaciones.
Un ejemplo genérico de un problema de programación lineal sería el siguiente:
![\displaystyle \mathbf{Restricciones:} \quad \left. \begin{array}{c} a_1 x+b_1y>c_1 \\[2ex] a_2 x+b_2y\leq c_2 \\ \vdots \end{array} \right\}](https://www.ejerciciosecuaciones.com/wp-content/ql-cache/quicklatex.com-b447953f2f20e72ada81437619147111_l3.svg "Rendered by QuickLaTeX.com")
La función a optimizar se suele llamar función objetivo.
Una vez ya sabemos qué es la programación lineal, veamos cómo se resuelven los problemas de programación lineal.
Cómo resolver un problema de programación lineal
Para resolver un problema de programación lineal se deben hacer los siguientes pasos:
- Identificar las incógnitas del problema.
- Hallar la función objetivo y las restricciones del problema.
- Representar todas las restricciones en una gráfica y determinar la región de validez (o zona de soluciones factibles) del problema.
- Determinar las coordenadas de todos los vértices de la región de validez y evaluar la función objetivo en cada uno de los vértices.
- El vértice en el que la función objetivo tome el mejor valor corresponde a la solución óptima del programa lineal.
Para acabar de entender cómo se solucionan los problemas de programación lineal, en el siguiente apartado hemos resuelto paso a paso un problema de este tipo a modo de ejemplo.
Ejemplo de un problema de programación lineal resuelto
A continuación, vamos a explicar paso a paso la resolución de un problema de programación lineal para que puedas ver un ejemplo de cómo se calculan:
- Una fábrica produce bicicletas de montaña, que las vende a 200€ cada una, y bicicletas de paseo, que las vende a 150€. Pero la fábrica solo dispone de 80 kg de acero y 120 kg de aluminio para fabricar. Además, para hacer una bicicleta de montaña se necesitan 1 kg de acero y 3 kg de aluminio, y para fabricar una bicicleta de paseo se necesitan 2 kg de acero y 2 kg de aluminio.
¿Cuántas bicicletas se deben fabricar para conseguir el máximo beneficio?
Lo primero que debemos hacer es identificar las incógnitas del problema, que en este caso son las siguientes:
En este ejercicio queremos maximizar el beneficio obtenido de las ventas de las bicicletas, por lo que el beneficio es la función a optimizar. Por cada bicicleta de montaña que vendamos ganaremos 200€ y por cada bicicleta de paseo 150€, por lo tanto, la función objetivo es:
Una vez tenemos la función a optimizar del problema, debemos encontrar las restricciones.
El enunciado dice que tan solo se pueden utilizar 80 kg de acero, cuando las bicicletas de montaña necesitan 1 kg y las de paseo 2 kg. Por tanto, debemos restringir el uso del acero mediante la siguiente inecuación:
Y lo mismo sucede con el aluminio, que únicamente se pueden usar 120 kg cuando cada bicicleta de montaña necesita 3 kg y cada bicicleta de paseo 2 kg. Por tanto, esta restricción pasada a forma de inecuación es:
Finalmente, aunque el enunciado no lo diga, es evidente que no se pueden fabricar unidades de bicicletas negativas, ya que no tiene sentido fabricar -50 bicicletas. De manera que también debemos añadir dos restricciones para que las unidades de bicicletas, tanto de montaña como de paseo, siempre sean cero o positivas:
![\begin{array}{c} x\ge 0 \\[2ex] y\ge 0 \end{array}](https://www.ejerciciosecuaciones.com/wp-content/ql-cache/quicklatex.com-7a0105642347d6c36b8315aa050e3379_l3.svg "Rendered by QuickLaTeX.com")
De modo que el problema de programación lineal queda definido por:
![\displaystyle \mathbf{Restricciones:} \quad \left. \begin{array}{c} x+2y \leq 80 \\[2ex] 3x+2y \leq 120 \\[2ex] x\ge 0 \\[2ex] y\ge 0 \end{array} \right\}](https://www.ejerciciosecuaciones.com/wp-content/ql-cache/quicklatex.com-b8a65b0970457cf47fb65750955f8a8b_l3.svg "Rendered by QuickLaTeX.com")
Ahora que tenemos todas las restricciones, debemos representarlas en una gráfica y determinar qué región de la gráfica cumple con todas las inecuaciones del sistema. Si no sabes cómo se hace, puedes ver el procedimiento explicado paso a paso en cómo resolver sistemas de inecuaciones con dos incógnitas.
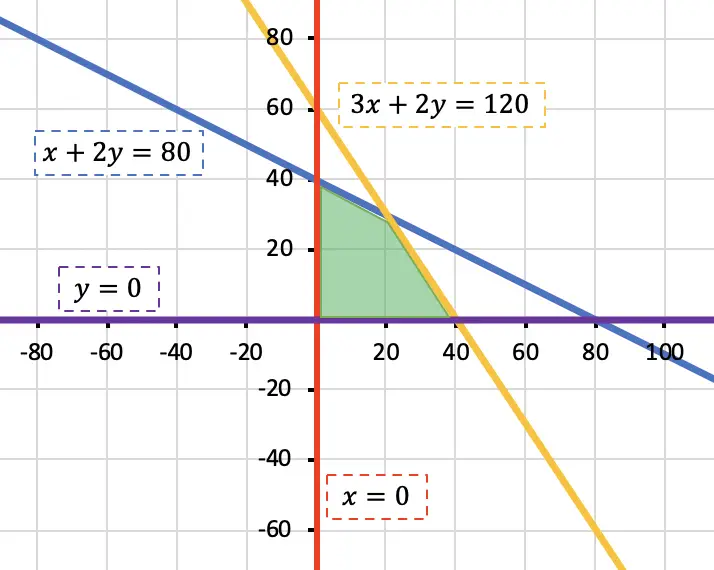
De modo que todos los puntos de la zona pintada de color verde son soluciones factibles del problema. Sin embargo, queremos encontrar la mejor solución posible, es decir, la solución óptima del problema. Esta siempre será uno de los vértices donde se cortan las rectas que limitan la región solución. Así que debemos encontrar las coordenadas cartesianas de los cuatro vértices de la zona verde.
Para hallar el punto en el que se cruzan dos rectas tenemos que solucionar el sistema de ecuaciones formado por esas dos rectas. Fíjate cómo encontramos el punto de corte entre la recta azul y la recta amarilla resolviendo el sistema de ecuaciones por el método de sustitución:
![\left. \begin{array}{l} x+2y=80 \\[2ex] 3x+2y=120 \end{array} \right\} \begin{array}{l} \longrightarrow \ x=80-2y \\[2ex] & \end{array}](https://www.ejerciciosecuaciones.com/wp-content/ql-cache/quicklatex.com-fbffdb56ee72bfd9ac2224eeb557925e_l3.svg "Rendered by QuickLaTeX.com")
De manera que el punto de intersección entre la recta azul y la recta amarilla es (20,30).
Ahora vamos a hallar las coordenadas de los otros vértices. El punto de intersección entre la recta azul y el eje Y es más fácil de calcular, porque el valor de la coordenada X en este eje siempre es igual a 0:
![\left. \begin{array}{l} x+2y=80 \\[2ex] x=0 \end{array} \right\} \begin{array}{l} \longrightarrow \ 0+2y=80 \\[2ex] & \end{array}](https://www.ejerciciosecuaciones.com/wp-content/ql-cache/quicklatex.com-f219541b129fbdb3d2127b3db5c377e3_l3.svg "Rendered by QuickLaTeX.com")
Lo mismo sucede con el punto que corta la recta amarilla con el eje X, ya que en este eje la coordenada Y siempre vale 0:
![\left. \begin{array}{l} 3x+2y=120 \\[2ex] y=0 \end{array} \right\} \begin{array}{l} \longrightarrow \ 3x+2\cdot 0=120 \\[2ex] & \end{array}](https://www.ejerciciosecuaciones.com/wp-content/ql-cache/quicklatex.com-e0e14e3ff8ce00f7c42430005ebeb48d_l3.svg "Rendered by QuickLaTeX.com")
Y finalmente tenemos como vértice el origen de coordenadas:
De manera que las coordenadas de los 4 vértices de la región de soluciones factibles son:
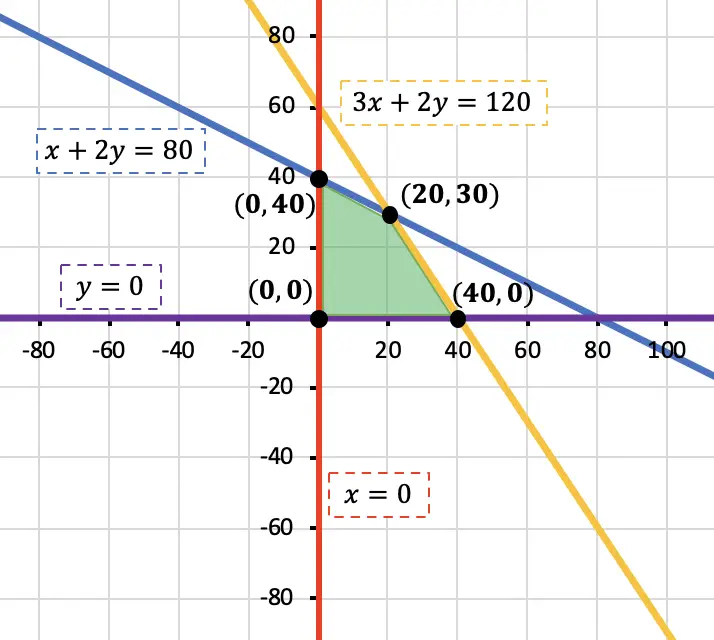
Ya solo nos queda el último paso para terminar el problema: sustituir cada vértice en la función objetivo. Procedemos a hacer los cálculos:
€
€
€
€
En este problema queremos maximizar el beneficio, es decir, la solución es el punto con el que obtenemos un mayor beneficio. Por lo tanto, debemos fabricar 20 bicicletas de montaña y 30 bicicletas de paseo para obtener el máximo beneficio posible, que es 8500€.
Ejercicios resueltos de programación lineal
Una vez hemos visto la teoría de la programación lineal, te dejamos con varios ejercicios resueltos de este tipo de problemas. Los problemas son de nivel de Bachillerato y están ordenados por dificultad.
👇👇👇¡Si tienes alguna duda sobre la resolución de algún ejercicio puedes escribirla en los comentarios!👇👇👇
Ejercicio 1
Una pastelería fabrica dos tipos de tartas. La tarta de tipo A se elabora con 1 kg de masa y 1,5 kg de chocolate, y se vende a 24 €. La de tipo B se elabora con 1,5 kg de masa y 1 kg de chocolate, y se vende a 30 €.
Si la pastelera solamente dispone de 300 kg de cada ingrediente, ¿cuántas tartas ha de fabricar de cada tipo para obtener el máximo ingreso? Calcula también el valor de dicho ingreso.
Primero de todo, debemos identificar las incógnitas del problema, que en este caso son las unidades de cada tipo de tarta fabricadas:
Luego tenemos que encontrar la función a optimizar, que en este caso es el ingreso obtenido. Por cada tarta del tipo A conseguimos 24 € y por cada tarta del tipo B 30 €, por tanto, los ingresos vienen definidos por la siguiente función:
Una vez hallada la función a optimizar, vamos a encontrar las inecuaciones que restringen el problema.
Solo disponemos 300 kg de masa, y de este ingrediente se necesitan 1 kg para cada tarta del tipo A y 1,5 kg para cada tarta del tipo B. Por tanto hay que restringir el uso de la masa mediante la siguiente desigualdad:
Y lo mismo sucede con el chocolate, que necesitamos 1,5 kg para cada tarta del tipo A y 1 kg para cada tarta del tipo B pero únicamente disponemos de 300 kg. Por tanto también debemos limitar su uso:
Lógicamente, no se pueden fabricar tartas negativas ya que no tiene sentido fabricar -30 tartas. De manera que también debemos añadir dos restricciones para que las tartas, tanto del tipo A como del tipo B, siempre sean cero o positivas:
En definitiva, el problema de programación lineal queda definido por:
![\displaystyle \mathbf{Restricciones:} \quad \left. \begin{array}{c} x+1,5y \leq 300 \\[2ex] 1,5x+y \leq 300 \\[2ex] x\ge 0 \\[2ex] y\ge 0 \end{array} \right\}](https://www.ejerciciosecuaciones.com/wp-content/ql-cache/quicklatex.com-307a3d35bae9dfe06bbc026ab4120981_l3.svg "Rendered by QuickLaTeX.com")
Ahora que tenemos todas las restricciones, las representamos en una gráfico, determinamos qué región de la gráfica cumple con todas las inecuaciones del sistema y calculamos las coordenadas de los vértices de dicha región:
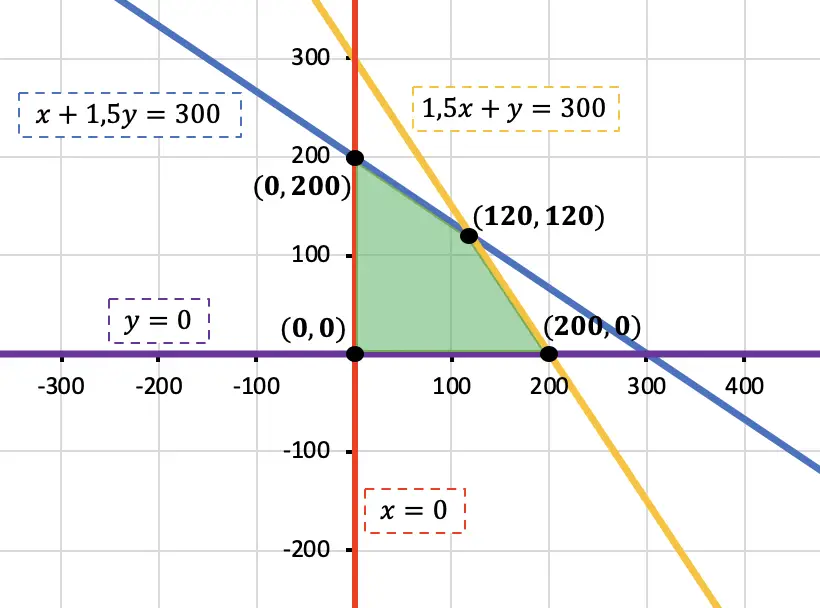
Por último, sustituimos cada vértice en la función objetivo para ver qué resultado es mejor:
€
€
€
€
En este problema queremos maximizar los ingresos, por tanto, la solución es el punto con el que obtenemos unos mayores ingresos. Por lo que debemos fabricar 120 tartas del tipo A y 120 tartas del tipo B para obtener el máximo ingreso posible, que es 6480€.
Ejercicio 2
Una compañía aérea quiere organizar un puente aéreo entre dos ciudades. Para ello necesita transportar como mínimo 1600 personas y 96 toneladas de equipaje y mercaderías. Además, para llevarlo a cabo, solo dispone de 11 aviones del tipo A, que pueden transportar 200 personas y 6 toneladas de equipaje cada uno, y 8 aviones del tipo B, que pueden transportar 100 personas y 15 toneladas cada uno.
Si la contratación de un avión de tipo A cuesta 4000€ y la de un avión del tipo B 1000€, calcula el número de aviones de cada tipo que hay que contratar para que el coste total sea mínimo y determina dicho coste.
En primer lugar, identificamos las incógnitas del problema, que en este caso son los aviones contratados de cada tipo:
Luego tenemos que encontrar la función objetivo del programa lineal, que en este caso es el coste de las contrataciones de los aviones. Cada avión del tipo A cuesta 4000€ y cada avión del tipo B 1000€, por lo tanto, los costes vienen definidos por la siguiente función:
Una vez hallada la función objetivo, pasamos a encontrar las inecuaciones que restringen el problema.
El enunciado dice que se deben transportar como mínimo 1600 personas, y cada avión de tipo A puede transportar 200 personas y cada avión de tipo B 100 personas. Por tanto:
Del mismo modo, el problema nos dice que se deben transportar como mínimo 6 toneladas de equipaje, y cada avión de tipo A puede transportar 6 toneladas y cada avión de tipo B 15 toneladas. Por tanto:
Por último, la contratación de los aviones es limitada: tan solo podemos contratar 11 aviones del tipo A y 8 aviones del tipo B. Así que debemos añadir estas dos restricciones:
![\begin{array}{c} x\leq 11 \\[2ex] y\leq 8 \end{array}](https://www.ejerciciosecuaciones.com/wp-content/ql-cache/quicklatex.com-cbf74dc4174ad4d948ff49957b0a553b_l3.svg "Rendered by QuickLaTeX.com")
En resumen, el problema de programación lineal queda definido por:
![\displaystyle \mathbf{Restricciones:} \quad \left. \begin{array}{c} 200x+100y \geq 1600 \\[2ex] 6x+15y \geq 96 \\[2ex] x\leq 11 \\[2ex] y\leq 8 \end{array} \right\}](https://www.ejerciciosecuaciones.com/wp-content/ql-cache/quicklatex.com-46b77630548d32410d338f0e39611629_l3.svg "Rendered by QuickLaTeX.com")
Ahora que tenemos todas las restricciones del problema, las representamos en un gráfico, determinamos qué región del gráfico cumple con todas las inecuaciones del sistema y calculamos las coordenadas de los vértices de dicha región:
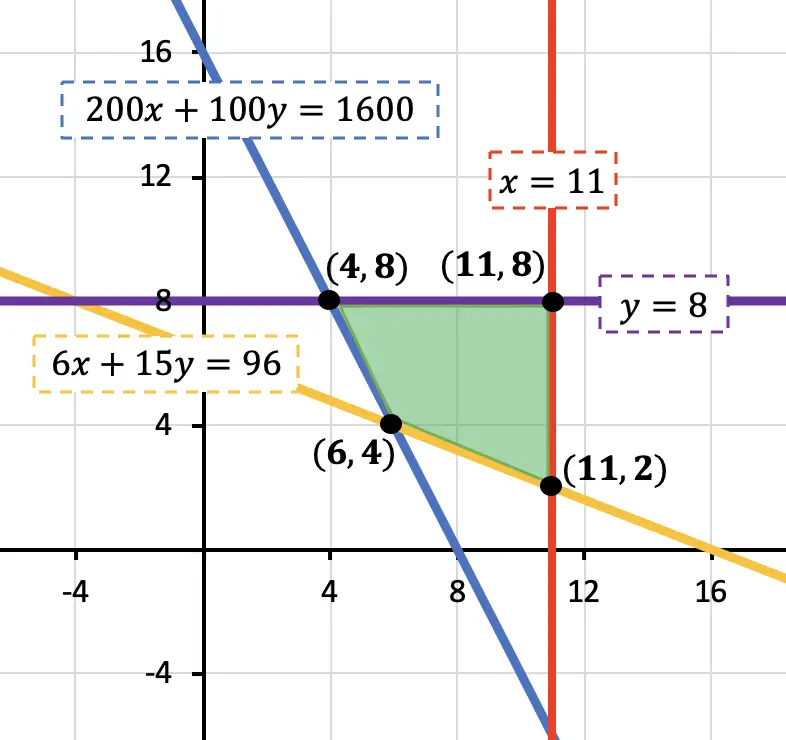
Finalmente, sustituimos cada vértice en la función objetivo de la programación lineal para ver qué resultado es el mejor:
€
€
€
€
En este problema queremos minimizar los costes, de forma que la solución es el punto con el que obtenemos un menor coste. En consecuencia, debemos contratar 4 aviones del tipo A y 8 aviones del tipo B para obtener el mínimo coste posible, que es 24000€.
Ejercicio 3
Una voluntaria quiere preparar helado artesano y horchata de auténtica chufa para un rastrillo solidario. La elaboración de cada litro de helado lleva 1 hora de trabajo y la elaboración de un litro de horchata 2 horas. Como la horchata no necesita leche, sabe que como máximo puede preparar hasta 15 litros de helado con la leche que tiene. Sin embargo, para que haya suficiente para todos los asistentes, tiene que preparar al menos 10 litros entre helado y horchata, en un máximo de 20 horas.
Si el beneficio por litro es de 25€ para el helado y 12€ para la horchata, calcula la cantidad de cada producto que se deberá preparar para maximizar el beneficio y calcula dicho beneficio máximo.
Primero de todo, debemos identificar las incógnitas del problema, que en este caso son los litros que se deben preparar de cada cosa:
Luego debemos averiguar la función a optimizar, que en este caso es el beneficio obtenido. Por cada litro de helado se consiguen 25€ y por cada litro de horchata 12€, así que el beneficio viene definido por la siguiente función:
Una vez hallada la función a optimizar, vamos a encontrar las inecuaciones que restringen el problema.
El enunciado dice que solo se pueden preparar 15 litros de helado. De manera que debemos limitar la producción de helado con la siguiente restricción:
Por otro lado, el problema nos dice que se deben preparar como mínimo 10 litros entre helado y horchata. Por tanto:
Además, nos dicen que todo se tiene que preparar en un máximo de 20 horas, y para hacer cada litro de helado se necesita 1 hora y para hacer un litro de horchata 2 horas. De manera que debemos añadir la siguiente restricción:
Evidentemente, no se pueden preparar litros negativos, así que también debemos añadir dos restricciones para que los litros de helado y de horchata siempre sean cero o positivos:
En conclusión, el problema de programación lineal queda definido por:
![\displaystyle \mathbf{Restricciones:} \quad \left. \begin{array}{c} x \leq 15 \\[2ex] x+y \geq 10 \\[2ex] x+2y \leq 20 \\[2ex] x\ge 0 \\[2ex] y\ge 0 \end{array} \right\}](https://www.ejerciciosecuaciones.com/wp-content/ql-cache/quicklatex.com-48158c6f885695b3d1cdc11b2ec66020_l3.svg "Rendered by QuickLaTeX.com")
Ahora que tenemos todas las restricciones del problema, las representamos en un gráfico, determinamos qué región del gráfico cumple con todas las inecuaciones del sistema y calculamos las coordenadas de los vértices de dicha región:
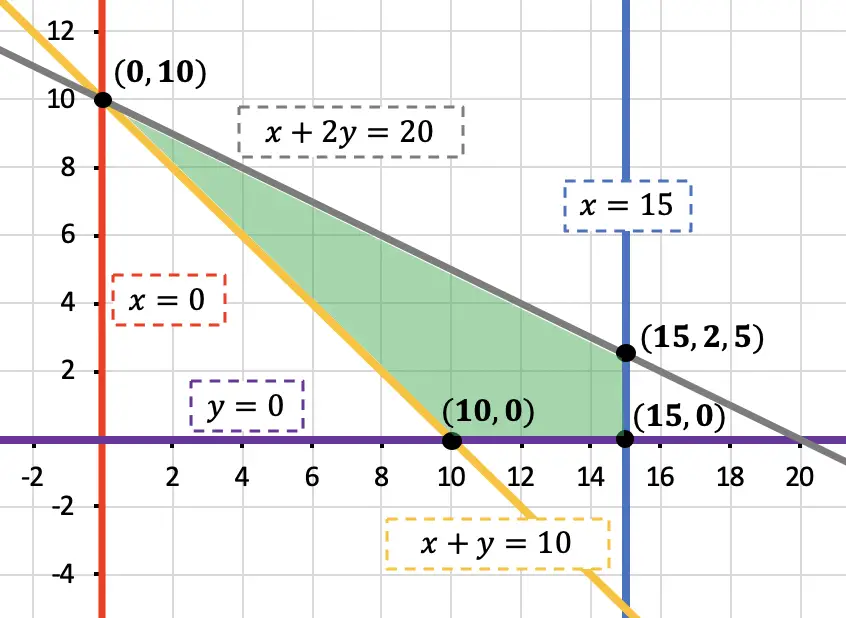
Este problema tiene una peculiaridad, porque hemos obtenido como solución factible el punto (15, 2,5). Sin embargo, no podemos vender 2,5 litros de horchata, sino que debe ser un número entero. Por tanto debemos coger (15,3) o (15,2). El punto (15,3) está fuera de la región factible, por lo tanto, cogeremos el punto (15,2).
Finalmente, para hallar la solución del problema de programación lineal, hacemos un análisis sustituyendo las coordenadas de los vértices en la función objetivo:
€
€
€
€
En este problema queremos maximizar el beneficio, por tanto, la solución óptima es el punto con el que obtenemos un mayor beneficio. De manera que el valor del programa lineal es 399€, que se consigue preparando 15 litros de helado y 12 litros de horchata.
Ejercicio 4
Una empresa textil quiere fabricar dos tipos de camisetas: lisas y estampadas. Para fabricar una camiseta lisa necesita 70 g de algodón y 20 g de poliéster, y para fabricar una camiseta estampada necesita 60 g de algodón y 10 g de poliéster. Actualmente, la empresa dispone para producir 4200 g de algodón y 800 g de poliéster. A parte, para que sea rentable debe fabricar al menos 10 camisetas estampadas y, además, el doble de las estampadas debe ser al menos igual al número de lisas.
Sabiendo que cada camiseta lisa da un beneficio de 5€ y cada estampada de 4€, ¿cuántas camisetas de cada tipo debería fabricar para obtener el máximo beneficio? ¿Cuál es ese beneficio?
Primero identificamos las incógnitas del problema:
Luego tenemos que encontrar la función a optimizar, que en este caso es el beneficio conseguido. Cada camiseta lisa vendida da un beneficio de 5€ y cada camiseta estampada 4€, por tanto, los beneficios están definidos por la siguiente función:
Una vez hallada la función a optimizar, vamos a encontrar las inecuaciones que restringen el problema.
Solo disponemos de 4200 g de algodón para fabricar, y cada camiseta lisa necesita 70 g de algodón y cada camiseta estampada 60 g de algodón. Por tanto:
Y lo mismo sucede con el poliéster, que necesitamos 20 g para cada camiseta lisa y 10 g para cada camiseta estampada, pero únicamente disponemos de 800 g de poliéster. Por tanto también debemos limitar su uso:
Aparte, el enunciado nos dice que para que sea rentable debemos fabricar al menos 10 camisetas estampadas. Por tanto:
Además, el problema dice que el doble de las camisetas estampadas producidas debe ser al menos igual al número de camisetas lisas. Por tanto:
Finalmente, aunque el enunciado del ejercicio no lo diga, es evidente que no se pueden fabricar camisetas negativas, ya que no tiene sentido fabricar -50 camisetas. De manera que también debemos añadir dos restricciones para que las camisetas, sean lisas o estampadas, siempre sean cero o positivas:
De modo que el problema de programación lineal queda definido por:
![\displaystyle \mathbf{Restricciones:} \quad \left. \begin{array}{c}70x+60y \leq 4200 \\[2ex] 20x+10y \leq 800 \\[2ex] y \geq 10 \\[2ex] 2y \geq x \\[2ex] x\ge 0 \\[2ex] y\ge 0 \end{array} \right\}](https://www.ejerciciosecuaciones.com/wp-content/ql-cache/quicklatex.com-42286753c03e69ee9bda945394690a96_l3.svg "Rendered by QuickLaTeX.com")
Una vez tenemos todas las restricciones del problema, las representamos gráficamente, determinamos qué región de la gráfica cumple con todas las inecuaciones del sistema y calculamos las coordenadas de los vértices de dicha región:
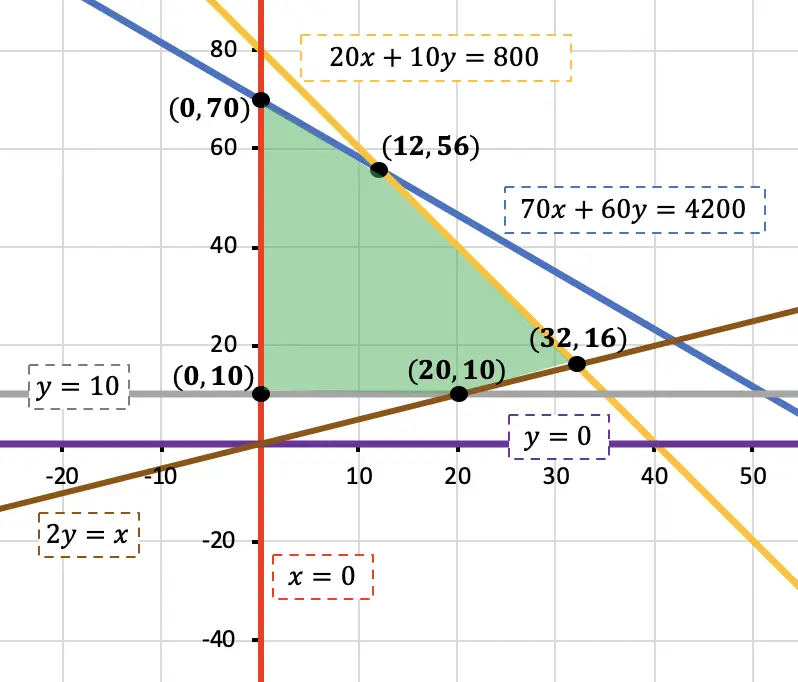
Para terminar de solucionar el problema, sustituimos cada vértice en la función a optimizar:
€
€
€
€
€
En este problema queremos maximizar el beneficio, por lo tanto, la solución óptima del programa lineal es el punto con el que obtenemos unos mayores beneficios. Por lo que debemos fabricar 12 camisetas lisas y 56 camisetas estampadas para obtener el máximo beneficio posible, que es 284€.
Ejercicio 5
Un agricultor quiere dedicar al menos 4 hectáreas al cultivo de dos productos: C1 y C2. Por cada hectárea del cultivo C1 se necesitan 20 horas de maquinaria y 100 kg de abono, y por cada hectárea del cultivo C2 se necesitan 10 horas de maquinaria y 300 kg de abono. Sin embargo, solo se dispone un total de 180 horas de maquinaria y 2400 kg de abono para esta temporada.
Además, el agricultor desea que el número de hectáreas dedicadas al cultivo C2 sea no menor que el número de hectáreas dedicadas al cultivo C1.
Si el beneficio neto obtenido por cada hectárea de C1 es de 3000€ y por cada hectárea de C2 es de 1500€, calcula las hectáreas que conviene dedicar a cada cultivo para que el beneficio total sea máximo y calcula dicho beneficio.
El primer paso para resolver el problema es identificar las incógnitas del problema, que son:
En segundo lugar, debemos hallar la función objetivo del problema, que en este caso es el beneficio obtenido. Por cada hectárea de C1 se consiguen 3000€ de beneficio y por cada hectárea de C2 1500€, por tanto, el beneficio neto viene definido por la siguiente función:
Una vez hallada la función a optimizar, vamos a encontrar las inecuaciones que restringen el problema.
El agricultor quiere cultivar como mínimo 4 hectáreas entre los productos C1 y C2. Por tanto:
Solo se dispone de 180 horas de maquinaria, y para cada hectárea de C1 se necesitan 20 horas y para cada hectárea de C2 10 horas. Por tanto hay que restringir el uso de las horas de máquina:
Y lo mismo sucede con el abono, que se necesitan 100 kg para cada hectárea de C1 y 300 kg para cada hectárea de C2, pero solo se dispone de 2400 kg de abono en total. Por lo tanto, también debemos limitar su uso:
Además, el agricultor desea que el número de hectáreas dedicadas al cultivo C2 sea no menor que el número de hectáreas dedicadas al cultivo C1. Por lo que también debemos añadir la siguiente restricción:
Finalmente, aunque el enunciado no lo diga, es evidente que no se pueden cultivar hectáreas negativas, ya que no tiene sentido cultivar -150 hectáreas. De manera que también debemos añadir dos restricciones para que las hectáreas, sean del cultivo C1 o del cultivo C2, siempre sean cero o positivas:
De modo que el problema de programación lineal queda definido por:
![\displaystyle \mathbf{Restricciones:} \quad \left. \begin{array}{c} x+y \geq 4 \\[2ex] 20x+10y \leq 180 \\[2ex] 100x+300y \leq 2400 \\[2ex] y \geq x \\[2ex] x\ge 0 \\[2ex] y\ge 0 \end{array} \right\}](https://www.ejerciciosecuaciones.com/wp-content/ql-cache/quicklatex.com-a10cac3a1ea1c70281f9ebef32af93b6_l3.svg "Rendered by QuickLaTeX.com")
Una vez tenemos todas las restricciones del problema, hacemos su representación gráfica, determinamos qué zona de la gráfica cumple con todas las inecuaciones del sistema y calculamos las coordenadas de los vértices de dicha región:
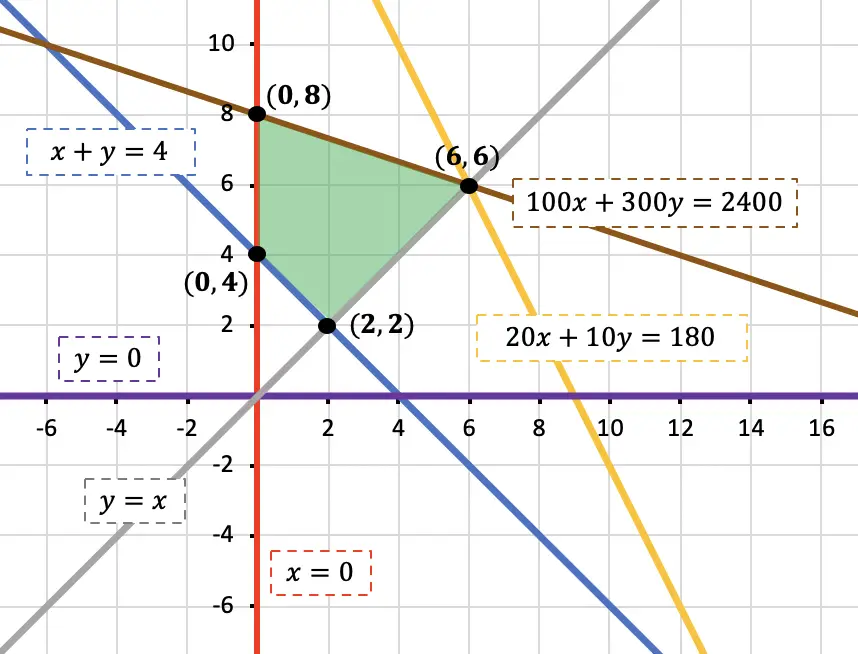
Finalmente, sustituimos cada vértice en la función objetivo del problema para ver qué resultado es el óptimo:
€
€
€
€
En este problema queremos maximizar el beneficio, por tanto, la solución es el punto con el que obtenemos un beneficio mayor. Entonces, debemos cultivar 6 hectáreas del producto C1 y 6 hectáreas del producto C2 para obtener el máximo beneficio posible, que es 27000€.
me ayudas con este problema, he seguido los pasos para solucionarlo pero siento que no son corretos.
Una escuela debe transportar 200 estudiantes a un evento. Hay disponibles tanto autobuses
grandes como pequeños. Un autobús grande tiene capacidad para 50 personas y alquilarlo
para el evento cuesta $800. Un autobús pequeño tiene capacidad para
40 personas y alquilarlo para el evento cuesta $600. Hay 8 conductores disponibles el día del evento.
Sí claro Claudia, entiendo que debes encontrar el número óptimo de autobuses grandes y pequeños.
En primer lugar, debes plantear las incógnitas del problema:
Luego encontramos todas las inecuaciones del problema y la función a optimizar:
Finalmente, representas todas las inecuaciones en una gráfica y evalúas la función objetivo en todos los puntos críticos. Y el resultado es aquel punto con el que se obtiene un valor de la función objetivo menor, pues queremos minimizar el coste de los autobuses:
De manera que para gastar el mínimo dinero posible se deben coger 5 autobuses pequeños y 0 autobuses grandes, y el coste será 3000$.
Una empresa que manufactura auto produce dos tipos a y b tiene dos fábricas f1 y f2 la primera produce 6 autos tipo a y 4 tipo b a un costo de $42000 diarios y funciona no más de 50 días la segunda produce 4 tipo y 4 tipo b a un costo de $34000 diarios, para cubrir la demanda deben vender al menos 360 autos del tipo A y al menos 300 del tipo b Cuántos días debe operar cada fábrica para que los costos sean mínimos y cuál es ese costo
Hola Daniela,
Las dos incógnitas que se necesitan para resolver el problema son las siguientes:
De manera que la función objetivo del problema es:
Entonces, a partir de la información proporcionada por el enunciado, planteamos todas las inecuaciones del problema:
Ahora representamos gráficamente todas las restricciones del problema y evaluamos la función objetivo en los puntos críticos. Como el objetivo es minimizar el coste, nos quedaremos con el punto que al evaluarlo en la función obtengamos el valor más bajo. Dicho punto es el siguiente:
En conclusión, la fábrica F1 debe operar 50 días y la fábrica F2 15 días.
Y en este no identificó muy bien las restricciones.
Un comerciante desea adquirir dos tipos de teléfono, TLF 1 y TLF 2 los tipos teléfono 1 cuestan 250$ y los tipo teléfono 2 cuestan 350 la unidad, tiene disponible 9000$ para adquirir los teléfonos y en su pequeño almacén solo dispone de espacio para 20 teléfonos, con la venta de cada teléfono gana el 30% del precio de la compra ¿ cuantos teléfonos puede adquirir para maximizar su beneficio?
Hola Daniela de nuevo,
Si decimos x e y a las unidades de cada tipo de teléfono:
En este caso, entendiendo que el 30% del precio de la compra es el beneficio obtenido y no los ingresos, para obtener la función objetivo debemos multiplicar los precios de compra por 0,3 por las unidades de cada teléfono:
Por otro lado, las restricciones del problema son:
Ahora, como en todos los problemas de este tipo, representamos las inecuaciones en un gráfico y evaluamos la función objetivo en cada punto crítico. Pero no este caso nos tenemos que quedar con el punto que maximice la función, que es:
Por lo tanto, debe ocupar todo su almacén con 20 teléfonos del tipo TLF 2. Es lógico que todos los teléfonos que deba comprar sean de este tipo, pues gana más dinero por vendiendo este tipo.
Me ayudas con este problema, he seguido los pasos para solucionarlo pero siento que no son correctos.
Un grupo de estudiantes desarrollan un emprendimiento y se dedican al negocio de la pastelería haciendo dos tipos de tortas; económica y clásica. Cada torta económica necesita un cuarto de relleno por cada kilogramo de bizcocho, mientras que una torta clásica necesita medio kilogramos de relleno por cada kilogramo de biscocho. En la pastelería se pueden hacer diariamente hasta 25kg de biscocho y 10kg de relleno. Así mismo para elaborar una torta económica se demoran una hora y media, pero para elaborar una torta clásica se demora dos horas y cuarto. Si desean sacar al mercado su producción acabo de dos días, y se sabe que cada torta económica produce un beneficio de 30 soles y la torta clásica 50 soles. ¿Cuántas tortas económicas y clásicas deberán elaborar para obtener el beneficio máximo?
Hola Mariana, te dejo la resolución del problema de programación lineal a continuación:
Las dos incógnitas del problema son el número de cada tipo de toras que deben elaborar:
La función a optimizar del problema es el beneficio que se obtiene con cada tarta, y su fórmula es:
![Ahora solamente nos queda hallar las restricciones del problema, que son las siguientes: [latex]\cfrac{1}{4}x+\cfrac{1}{2}y\le10](https://www.ejerciciosecuaciones.com/wp-content/ql-cache/quicklatex.com-aee2975ba709e56a3a5403173574567d_l3.svg "Rendered by QuickLaTeX.com")
Por último, al igual que en todos los problemas de programación lineal, representamos gráficamente las inecuaciones y evaluamos la función objetivo en los extremos de la región permitida. Lógicamente, como queremos maximizar el beneficio económico nos quedamos con el punto en el cual el valor de la función sea mayor, que es:
[latex}f(8,16)=30\cdot 8+50\cdot 16=1040[/latex]
De manera que se deben hacer 8 tartas económicas y 16 tartas clásicas.
4. Una empresa acaba de inaugurar una planta nueva que fabricará más de 500 productos diferentes, usando más de 50 líneas de producción y máquinas distintas. Las decisiones de programación de la producción son cruciales, ya que las ventas se perderán si la demanda de los clientes no se satisface a tiempo. Si nadie en la empresa ha tenido experiencia con esta operación de producción, y cada semana se deben generar programas de producción nuevos. Considere 40 horas semanales
Sin embargo, no logro plantear el modelo
Hola Claudia,
Se trata de un problema de programación lineal avanzada. Para plantear el modelo primero deberías saber qué se quiere minimizar o maximizar para poder hacer la función objetivo. Además, faltan datos como por ejemplo cuánto se tarda en fabricar cada tipo de producto, si depende de la máquina en la que se produce, o el número máximo de personal.
Gracias por tu explicación, muy didáctica, muy clara. Aprendí bastante, Tal vez puedas enviarme un ejercicio con más variables: por ejemplo 5 ó 6.
¡Muchas gracias Néstor!
Un ejercicio con tantas variables ya sería un ejercicio de programación lineal avanzada, este artículo se centra en un nivel de programación lineal de menor nivel. De todos modos, gracias por proponer la idea, ¡la apunto para hacer un post en el futuro!
Excelente trabajo. bien explicados y se puede entender la función de la investigación de operaciones. Gracias.
¡Gracias a ti por el comentario Juan Manuel!
Gracias por ayudarnos a entender los ejercicios!!! Muchas gracias!!!
¡Gracias a ti por el comentario Ale y por usar esta página web!
Hola! me ayudarías con esta duda?
Usando de ejemplo el ejercicio 5; cómo resolvemos la restricción Y ≥ X?
No logro entender que hacemos para encontrarlas.
Gracias!
Hola Yael,
y=x es una recta que pasa por el origen de coordenadas y su pendiente es igual a la unidad, de modo que la y aumenta una unidad cuando la x aumenta una unidad.
Así pues, la condición y≥x la cumplen todos aquellos puntos que estén por encima de la recta y=x.