▷ Inecuaciones con valor absoluto

En este post te explicamos qué es una inecuación con valor absoluto y cómo se resuelve. Además, podrás practicar con varios ejercicios resueltos paso a paso de inecuaciones con valores absolutos.

Índice

¿Qué son las inecuaciones con valor absoluto?

Las inecuaciones con valor absoluto son desigualdades algebraicas en las que incógnita aparece en el argumento de una función con valor absoluto.

Las inecuaciones con valor absoluto también se llaman inecuaciones con módulo.

Las inecuaciones con valor absoluto se resuelven de manera similar a las ecuaciones con valor absoluto, aunque evidentemente unas son igualdades y otras desigualdades.

Cómo resolver inecuaciones con valor absoluto

Para resolver una inecuación con valor absoluto se deben seguir los siguientes pasos:

Despejar el valor absoluto en un miembro de la inecuación.
Negar el otro miembro de la inecuación para obtener dos inecuaciones sin valor absoluto:
- Una primera inecuación sin ese miembro negado.
- Y una segunda inecuación con el segundo miembro negado y el sentido de la desigualdad girado.
Resolver cada inecuación obtenida por separado
El conjunto solución de la inecuación con valor absoluto es la unión de las dos soluciones calculadas en el paso anterior.

Para acabar de entender cómo se calculan las inecuaciones con valor absoluto, en el siguiente apartado hemos resuelto por pasos una inecuación de este tipo a modo de ejemplo. Sin embargo, antes de ver el ejemplo te recomiendo ver cuáles son las propiedades del valor absoluto, ya que te ayudará a resolver este tipo de inecuaciones.

Propiedades del valor absoluto

Empecemos por la definición de valor absoluto, que indica que su argumento siempre es positivo o igual a 0:

$\lvert x\rvert \geq 0$

$\lvert -5\rvert = 5$

El valor absoluto del producto de dos factores es equivalente al producto del valor absoluto de cada factor por separado:

$\lvert x\cdot y\rvert =\lvert x\rvert\cdot\lvert y\rvert$

Lo mismo sucede con el cociente entre dos números. El valor absoluto de una división es lo mismo que primero hacer el valor absoluto de cada término y luego dividirlos:

$\displaystyle\displaystyle\left|\frac{x}{y}\right| =\frac{\lvert x\rvert}{\lvert y\rvert }$

En cambio, el valor absoluto de la suma de dos términos cumple la siguiente desigualdad:

$\lvert x+y\rvert\leq \lvert x\rvert +\lvert y\rvert$

Por último, las siguientes dos propiedades del valor absoluto son las que más se utilizan para resolver inecuaciones con valor absoluto:

$\lvert x\rvert\leq k \iff -k\leq x\leq k$

$\lvert x\rvert\geq k \iff \begin{cases}x\geq k\\[2ex] x\leq -k\end{cases}$

Ejemplo de inecuación con valor absoluto resuelta

Vista la teoría de las inecuaciones con valor absoluto, vamos a explicar paso a paso la resolución de una inecuación con valor absoluto como ejemplo:

$\left|2x+3\right|-5\geq 0$

Lo primero que debemos hacer es despejar el valor absoluto en un lado de la inecuación:

$\left|2x+3\right|\geq 5$

En segundo lugar, debemos negar el miembro de la inecuación que no tiene el valor absoluto. De este modo conseguiremos dos inecuaciones sin valor absoluto: una inecuación con el segundo miembro positivo, y otra inecuación con el segundo miembro negativo y el sentido de la desigualdad girado.

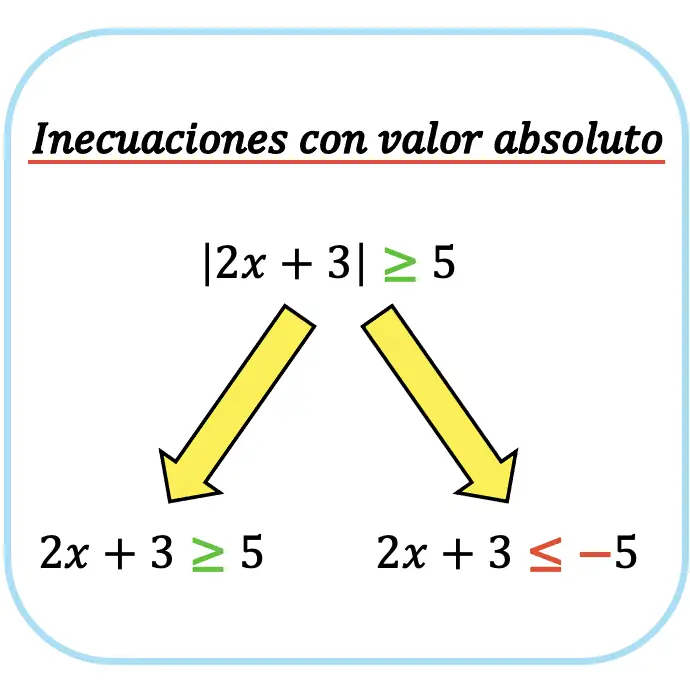
Este paso se hace porque en realidad el interior del valor absoluto puede ser igual a un número positivo o un número negativo, ya que el valor absoluto transforma su argumento en positivo. En consecuencia, se deben hallar los valores de x que cumplen la inecuación dando un resultado positivo y los que cumplen la inecuación dando un resultado negativo.

Una vez tenemos las dos inecuaciones, resolvemos cada una por separado:

$2x+3\geq 5$

$2x\geq 5-3$

$2x\geq 2$

$x\geq \cfrac{2}{2}$

$x\geq 1$

$2x+3\leq -5$

$2x\leq -5-3$

$2x\leq -8$

$x\leq \cfrac{-8}{2}$

$x\leq -4$

Por lo tanto, la solución de la inecuación es la unión de las dos soluciones obtenidas en el paso anterior:

$x\geq 1 \ \cup \ x\leq -4$

Entonces, la representación gráfica de la solución de la inecuación es la siguiente:

Como puedes ver, hemos representado los números con puntos cerrados, porque la solución tiene los signos ≥ y ≤ que incluyen el igual. Pero si la solución hubiera tenido los signos sin el igual (> y <), deberíamos haber representado los puntos abiertos ya que los puntos no estarían incluidos.

Y, finalmente, los intervalos que representan la solución de la inecuación con valor absoluto son:

$x\in (-\infty,-4]\cup[1,+\infty)$

Ejercicios resueltos de inecuaciones con valor absoluto

Ejercicio 1

Calcula la siguiente inecuación de primer grado con valor absoluto:

$\left|x-1\right|-2<0$

Ver solución

Primero de todo, aislamos el valor absoluto en un miembro de la inecuación:

$\left|x-1\right|<2$

Ahora negamos el miembro de la inecuación sin valor absoluto. De esta forma obtendremos dos desigualdades sin valor absoluto: una desigualdad con el segundo miembro positivo, y otra desigualdad con el segundo miembro negativo y el signo cambiado.

$\left|x-1\right|<2 \ \longrightarrow \ \begin{cases}x-1<2\\[2ex]x-1>-2\end{cases}$

Una vez tenemos las dos inecuaciones, solucionamos cada una por separado:

$x-1<2$

$x<2+1$

$x<3$

$x-1>-2$

$x>-2+1$

$x>-1$

De manera que conjunto solución de la inecuación es la unión de las dos soluciones obtenidas:

$x<3 \ \cup \ x>-1$

Representamos gráficamente la solución obtenida:

Y, por último, el intervalo solución de la inecuación con valor absoluto es:

$x\in (-1,3)$

Ejercicio 2

Determina la solución de la siguiente inecuación con valor absoluto:

$\left|3x+8\right|-6<5x$

Ver solución

En primer lugar, despejamos el valor absoluto en un lado de la desigualdad:

$\left|3x+8\right|<5x+6$

Luego negamos el segundo miembro de la inecuación para así obtener dos inecuaciones sin valor absoluto: una inecuación con el segundo miembro positivo, y otra inecuación con el segundo miembro negativo y el signo cambiado.

$\left|3x+8\right|<5x+6 \ \longrightarrow \ \begin{cases}3x+8<5x+6\\[2ex]3x+8>-5x-6\end{cases}$

Ahora calculamos cada inecuación por separado:

$3x+8<5x+6$

$3x-5x<6-8$

$-2x<-2$

$x>\cfrac{-2}{-2}$

$x>1$

Recuerda que cuando en una inecuación cambiamos de lado un término negativo que está multiplicando o dividiendo también debemos cambiar el sentido de la desigualdad.

$3x+8>-5x-6$

$3x+5x>-6-8$

$8x>-14$

$x>\cfrac{-14}{8}$

$x>\cfrac{-7}{4}$

En este problema, de las dos subinecuaciones hemos obtenido una solución que incluye la otra solución, por tanto, la solución global de la inecuación con valor absoluto será aquella que es más restrictiva:

$x>1$

Representamos gráficamente la solución obtenida:

Y el intervalo solución de la inecuación con valor absoluto es:

$x\in (1,+\infty)$

Ejercicio 3

Soluciona la siguiente inecuación con valor absoluto:

$\left|3x-9\right|\leq 0$

Ver solución

En este caso ya tenemos la expresión con valor absoluto despejada. Por lo que simplemente tenemos que hacer el paso de negar el segundo miembro para obtener dos inecuaciones diferentes:

$\left|3x-9\right|\leq 0 \ \longrightarrow \ \begin{cases}3x-9\leq0\\[2ex]3x-9\geq0\end{cases}$

En segundo lugar, resolvemos cada desigualdad por separado:

$3x-9\leq0$

$3x\leq9$

$x\leq\cfrac{9}{3}$

$x\leq3$

$3x-9\geq0$

$3x\geq9$

$x\geq\cfrac{9}{3}$

$x\geq3$

Entonces, la solución de la inecuación con valor absoluto es la unión de las dos soluciones obtenidas:

$x\leq3 \ \cup \ x\geq3$

Pero en este caso solamente hay un valor que cumpla con los dos intervalos, que es el número 3:

$x=3$

Así que la inecuación con valor absoluto tiene una única solución.

Por otro lado, ten en cuenta que si la inecuación a resolver hubiera sido |3x-9|<0, sería una inecuación sin solución. Porque el valor absoluto de una expresión algebraica nunca puede ser negativo.

Ejercicio 4

Resuelve la siguiente inecuación de segundo con valor absoluto:

$\left|x^2-4\right|\geq 5$

Ver: cómo resolver inecuaciones cuadráticas

Ver solución

El valor absoluto ya está despejado en un miembro de la inecuación. Por tanto, negamos directamente el segundo miembro para obtener dos inecuaciones:

$\left|x^2-4\right|\geq 5 \ \longrightarrow \ \begin{cases}x^2-4\geq5\\[2ex]x^2-4\leq -5\end{cases}$

Ahora tenemos que resolver cada inecuación de segundo grado por separado. Si no entiendes el procedimiento que haremos a continuación, te recomendamos que visites el enlace de arriba y veas cómo se resuelven este tipo de inecuaciones.

$x^2-4\geq5$

$x^2-4=5$

$x^2=9$

$x=\pm 3$

$x\in (-\infty,-3)\cup (3,+\infty)$

$x^2-4\leq -5$

$x^2=-5+4$

$x^2=-1$

$x=\sqrt{-1} \ \color{red}\bm{\times}$

Ningún término de la recta real cumple con esta inecuación, por lo que esta inecuación no tiene solución.

En conclusión, la solución de la inecuación cuadrática con valor absoluto es equivalente a la solución calculada con la primera subinecuación:

$x\in (-\infty,-3)\cup (3,+\infty)$

Ejercicio 5

Resuelve la siguiente inecuación racional con valor absoluto:

$\displaystyle\left|\frac{3x-1}{x}\right|\geq 4$

Ver: cómo resolver inecuaciones racionales

Ver solución

En primer lugar, negamos el segundo miembro de la inecuación para obtener dos desigualdades distintas y poder quitar el valor absoluto:

$\displaystyle\left|\frac{3x-1}{x}\right|\geq 4 \ \longrightarrow \ \begin{cases}\displaystyle\frac{3x-1}{x}\geq 4\\[4ex]\displaystyle\frac{3x-1}{x}\leq -4\end{cases}$

Y resolvemos cada inecuación fraccionaria obtenida por separado:

$\displaystyle\frac{3x-1}{x}\geq 4$

$\displaystyle\frac{3x-1}{x}-4 \geq 0$

$\displaystyle\frac{3x-1}{x}-\cfrac{4\cdot x}{x} \geq 0$

$\displaystyle\frac{3x-1-4x}{x} \geq 0$

$\displaystyle\frac{-x-1}{x} \geq 0$

$\begin{cases}-x-1=0 \ \longrightarrow \ x=-1 \\[2ex] x=0 \end{cases}$

Ahora evaluamos la inecuación en los tramos que resultan de dividir la recta real entre los puntos críticos hallados. Y la solución de esta subinecuación racional es:

$x\in [-1,0)$

$\displaystyle\frac{3x-1}{x}\leq -4$

$\displaystyle\frac{3x-1}{x}+4 \leq 0$

$\displaystyle\frac{3x-1}{x}+\cfrac{4\cdot x}{x} \leq 0$

$\displaystyle\frac{3x-1+4x}{x} \leq 0$

$\displaystyle\frac{7x-1}{x} \leq 0$

$\begin{cases}7x-1=0 \ \longrightarrow \ x=\cfrac{1}{7} \\[2ex] x=0 \end{cases}$

Ahora evaluamos la inecuación en los tramos que resultan de dividir la recta real entre los puntos críticos hallados. Y la solución de esta subinecuación racional es:

$\displaystyle x\in \left(0,\frac{1}{7}\right]$

Entonces, la solución de la inecuación racional con valor absoluto es la unión de las dos soluciones obtenidas, que representadas en la recta numérica son:

Y los intervalos que definen la solución de la inecuación con valor absoluto del problema son:

$\displaystyle x\in [-1,0) \ \cup \ \left(0,\frac{1}{7}\right]$

Inecuaciones con valor absoluto

¿Qué son las inecuaciones con valor absoluto?

Cómo resolver inecuaciones con valor absoluto

Ejemplo de inecuación con valor absoluto resuelta

Ejercicios resueltos de inecuaciones con valor absoluto

Ejercicio 1

Ejercicio 2

Ejercicio 3

Ejercicio 4

Ejercicio 5

2 comentarios en “Inecuaciones con valor absoluto”

Deja un comentario Cancelar respuesta