Ecuaciones con valor absoluto

Aquí te explicamos cómo se resuelven las ecuaciones con valor absoluto. Además, encontrarás varios ejercicios resueltos paso a paso de ecuaciones con valor absoluto para poder practicar.

Cómo resolver ecuaciones con valor absoluto

Para resolver una ecuación con valor absoluto se deben seguir los siguientes pasos:

1. Despejar el valor absoluto en un miembro de la ecuación.
2. Negar el otro miembro de la ecuación para obtener dos ecuaciones: la primera con ese miembro negado, y la segunda con ese miembro sin negar.
3. Resolver las dos ecuaciones obtenidas en el paso anterior.
4. Comprobar las soluciones halladas sustituyendo sus valores en la ecuación original.

Ten en cuenta que las ecuaciones con valor absoluto también se pueden llamar ecuaciones con módulo.

Ejemplo de una ecuación con valor absoluto resuelta

Para que quede claro cómo se hacen este tipo de ecuaciones, a continuación veremos la resolución de una ecuación con valor absoluto paso a paso como ejemplo:

Lo primero que debemos hacer es despejar la expresión con valor absoluto. Así que movemos de miembro el término -5 cambiando su signo:

En segundo lugar, debemos negar el miembro de la ecuación que no tiene el valor absoluto. De esta manera conseguiremos dos ecuaciones: una ecuación con el segundo miembro positivo, y otra ecuación con el segundo miembro negativo.

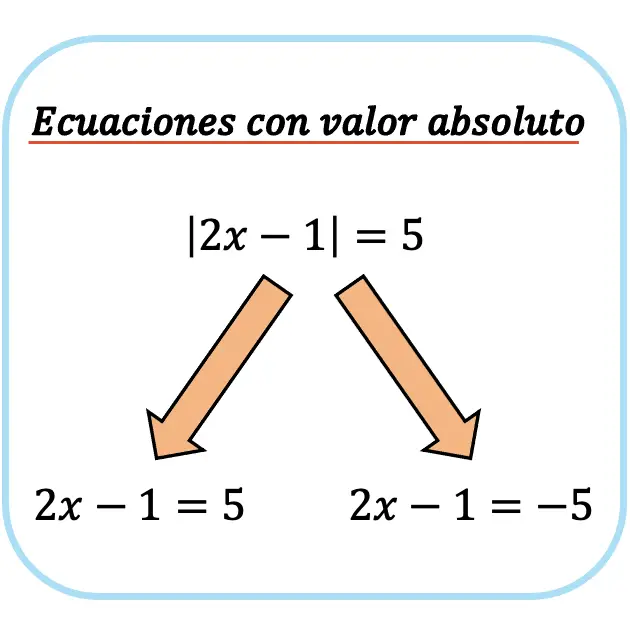
Este paso se hace porque en realidad el interior del valor absoluto puede ser igual a un número positivo o un número negativo, ya que el valor absoluto transforma su argumento en positivo. En consecuencia, se deben hallar los valores de x que cumplen la ecuación dando un resultado positivo y los que cumplen la ecuación dando un resultado negativo.

Y, una vez tenemos las dos ecuaciones, debemos resolver cada una por separado:

Por lo tanto, la ecuación tiene dos posibles soluciones, que son x=3 y x=-2.

Ahora tenemos que comprobar si las dos son soluciones de la ecuación con valor absoluto. Para ello, sustituimos cada valor obtenido en la ecuación original y miramos si se cumple la igualdad:

Las dos soluciones halladas verifican la ecuación con valor absoluto, por lo tanto, ambas son soluciones de la ecuación. Esta condición se puede expresar de la siguiente manera:

En este caso, las dos soluciones obtenidas eran soluciones verdaderas de la ecuación. Sin embargo, podría ser que alguna de ellas no fuera solución, o incluso, que ninguna de las dos lo fuera.

Ahora que ya has visto cómo se calculan las ecuaciones con valor absoluto, te recomendamos que veas cómo resolver inecuaciones con valor absoluto. El procedimiento es prácticamente igual, pero hay algunos detalles importantes en las inecuaciones.

Ejercicios resueltos de ecuaciones con valor absoluto

Ejercicio 1

Resuelve la siguiente ecuación con valor absoluto:

Primero de todo, despejamos el valor absoluto en un miembro de la ecuación:

Y luego negamos el miembro de la ecuación sin el valor absoluto, para así obtener dos ecuaciones: una ecuación con el segundo miembro positivo, y otra ecuación con el segundo miembro negativo.

Ahora resolvemos las 2 ecuaciones por separado:

De modo que la ecuación tiene dos posibles soluciones, x=5 y x=-2. Pero debemos verificar si realmente son soluciones de la ecuación. Y, para ello, sustituimos cada valor en la ecuación original y miramos si se cumple la igualdad:

Las dos soluciones calculadas verifican la igualdad, por lo tanto, el conjunto solución de la ecuación con valor absoluto es:

 

Ejercicio 2

Soluciona la siguiente ecuación con valor absoluto:

Primero despejamos el valor absoluto en un lado de la ecuación:

Después, negamos el lado de la ecuación que no tiene valor absoluto. Resultando así dos ecuaciones: una ecuación con el segundo lado positivo, y otra ecuación con el segundo lado cambiado de signo.

Solucionamos las dos ecuaciones resulantes:

Sustituimos cada solución obtenida en la ecuación original para comprobar si realmente son solución:

En este problema x=-1 sí que cumple la ecuación original, en cambio, x=5 no la cumple. Con lo que la única solución de la ecuación con valor absoluto es x=-1.

 

Ejercicio 3

Calcula la siguiente ecuación con valor absoluto:

Como siempre en este tipo de ecuaciones, primero debemos despejar el valor absoluto en un miembro de la ecuación:

Sin embargo, en este caso nunca se cumplirá la ecuación, porque el valor absoluto de la izquierda de la ecuación nunca equivaldrá a -5, ya que del valor absoluto siempre saldrá un número positivo. Por lo tanto, se trata de una ecuación con valor absoluto sin solución.

 

Ejercicio 4

Resuelve la siguiente ecuación con valor absoluto en ambos lados:

Aunque la ecuación tenga valor absoluto en los dos miembros, debemos aplicar el mismo procedimiento. Por tanto, tenemos que solucionar una ecuación con ambos valores absolutos positivos, y otra ecuación con un valor absoluto cambiado de signo:

Resolvemos las dos ecuaciones obtenidas:

Y, finalmente, comprobamos ambas soluciones sustituyéndolas en la ecuación original:

Las dos soluciones halladas cumplen la igualdad, de forma que el conjunto solución de la ecuación con valor absoluto es:

 

También te puede interesar:

• Qué son las ecuaciones equivalentes
• Qué son las ecuaciones cuadráticas incompletas
• Qué son las ecuaciones bicuadradas
• Qué son las ecuaciones irracionales
• Qué son las ecuaciones fraccionarias