En este post se explica qué es una ecuación de primer grado y cómo se resuelve. Además, encontrarás varios ejercicios resueltos paso a paso de ecuaciones de primer grado para practicar.
Índice
¿Qué son las ecuaciones de primer grado?
Las ecuaciones de primer grado son igualdades algebraicas en las cuales la incógnita (normalmente x) está elevada a la 1. De modo que para resolver ecuaciones de primer grado primero se deben sumar términos similares y luego despejar la incógnita de la ecuación.
Las ecuaciones de primer grado también se llaman ecuaciones lineales.
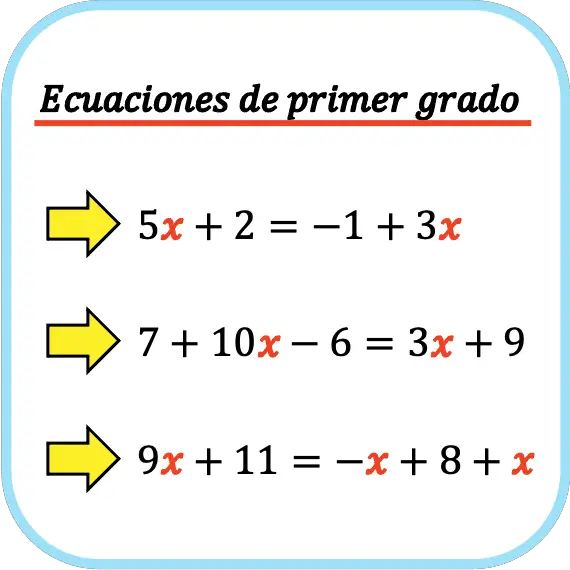
En general, las ecuaciones de primer grado se suelen trabajar en los cursos iniciales de matemáticas de secundaria, ya que sirven para entender muchos conceptos de álgebra lineal. Asimismo, también se suelen hacer problemas con ecuaciones de primer grado para practicar.
Cómo resolver ecuaciones de primer grado
Los pasos para resolver una ecuación de primer grado son:
- Trasponer términos de la ecuación de primer grado: colocar los términos con incógnita en un miembro de la ecuación y los términos sin incógnita en el otro miembro.
- Agrupar los términos semejantes: sumar (o restar) los términos de cada miembro de la ecuación de primer grado.
- Despejar la incógnita: pasar el coeficiente del término con incógnita al otro miembro de la ecuación dividiendo y calcular la división resultante.
Para que veas cómo se hace, en el siguiente apartado tienes una ecuación de primer grado resuelta paso a paso.
Ejemplo de una ecuación de primer grado resuelta
Ahora que ya hemos visto la teoría de las ecuaciones de primer grado, a continuación tienes un ejemplo resuelto de una ecuación de primer grado con una incógnita.
Primero de todo, tenemos que pasar los términos con x a un lado de la ecuación y los términos sin incógnita al otro lado de la ecuación. En este caso, pondremos todos los elementos con x en el lado izquierdo y los números sin x en el lado derecho:
![\begin{array}{l}3x\color{red}\bm{+4}\color{black}=\color{blue}\bm{2x}\color{black}-5\definecolor{verd}{HTML}{2ECC71}\color{verd}\bm{-8x}\color{black}\\[3ex]3x\color{blue}\bm{-2x}\color{black}\definecolor{verd}{HTML}{2ECC71}\color{verd}\bm{+8x}\color{black}=\color{red}\bm{-4}\color{black}-5\end{array}](https://www.ejerciciosecuaciones.com/wp-content/ql-cache/quicklatex.com-e93ffcc27f847a462b050be7b2fb79f6_l3.svg "Rendered by QuickLaTeX.com")
Fíjate que para cambiar un término de lado de la ecuación se debe cambiar su signo:
➤ Si un término está sumando en un lado de la ecuación, pasa restando al otro lado de la ecuación.
➤ Si un término está restando en un lado de la ecuación, pasa sumando al otro lado de la ecuación.
Una vez ya tenemos todos los términos ordenados, tenemos que sumar (o restar) todos los términos del mismo lado. Así pues, hacemos las operaciones de cada lado de la ecuación:
Ahora solo nos queda despejar la incógnita de la ecuación de primer grado. Para ello, pasamos el coeficiente de la x dividiendo al otro lado de la ecuación:
Y, finalmente, resolvemos la división:
En definitiva, la solución de la ecuación de primer grado es -1. Sin embargo, debes tener presente que algunas ecuaciones no tienen solución. Puedes ver cuándo una ecuación no tiene solución haciendo clic aquí:
➤ Ver: ecuaciones sin solución
Ejercicios resueltos de ecuaciones de primer grado
Ejercicio 1
Resuelve la siguiente ecuación de primer grado:
En primer lugar, pasamos los términos con x al miembro izquierdo de la ecuación y los números sin x al miembro derecho. Ten presente que al cambiar de miembro un término se debe cambiar su signo:
Ahora agrupamos los términos de cada miembro de la ecuación de primer grado:
Por último, despejamos la x pasando su coeficiente al otro lado dividiendo:
Y resolvemos la división resultante:
Ejercicio 2
Halla la x de la siguiente ecuación de primer grado:
Primero colocamos los términos con x en el lado izquierdo de la ecuación y los términos sin x en el lado derecho. Recuerda que al cambiar un término de lado también se debe cambiar su signo:
En segundo lugar, hacemos las sumas algebraicas de los dos lados de la ecuación:
Y, finalmente, despejamos la x de la ecuación de primer grado:
Ejercicio 3
Despeja la x de la siguiente ecuación de primer grado:
El primer paso para resolver ecuaciones de primer grado es pasar todos los términos similares al mismo lado de la ecuación. Así pues, ponemos todos los términos con incógnita a la izquierda y todos los otros términos a la derecha:
Luego hacemos las sumas o restas de cada lado de la ecuación
Sin embargo, en este caso la ecuación nunca se podrá cumplir, ya que 0 no es equivalente a -25. Es decir, independientemente del valor de la x, nunca se cumplirá la igualdad. Por lo tanto, es una ecuación de primer grado sin solución.
Para saber más acerca de las ecuaciones sin soluciones, puedes consultar el artículo enlazado más arriba.
Ejercicio 4
Calcula el valor de la x para que se cumpla la siguiente ecuación de primer grado:
El primer paso para determinar la solución de una ecuación de primer grado es pasar todos los términos con x a un lado y los otros términos al lado opuesto. Teniendo en cuenta que al cambiar de lado un término también se debe cambiar su signo, la ecuación queda:
Ahora agrupamos los términos de los dos miembros de la ecuación:
Para terminar, despejamos la incógnita de la ecuación de primer grado:
Ejercicio 5
Encuentra la solución de la siguiente ecuación de primer grado:
Primero pasamos los términos con incógnita al miembro izquierdo de la ecuación y los términos sin incógnita al otro miembro de la ecuación:
En segundo lugar, sumamos los términos de cada miembro de la ecuación:
Despejamos la incógnita de la ecuación:
Y, finalmente, simplificamos la fracción al máximo:
Ecuaciones de primer grado con paréntesis
A lo largo de este artículo has visto cómo se resuelven las ecuaciones de primer grado sencillas, es decir, sin paréntesis y sin fracciones. Sin embargo, debes saber que las ecuaciones de primer grado pueden ser más complicadas.
Por ejemplo, a continuación puedes ver una ecuación de primer grado con dos paréntesis:
Así pues, para resolver una ecuación de primer grado con paréntesis, primero debes calcular las operaciones de los paréntesis y luego solucionar la ecuación como si fuera una ecuación normal.
Por lo tanto, las ecuaciones de primer grado con paréntesis son un poco más difíciles que las ecuaciones de los ejercicios de arriba ya que se deben hacer más pasos para resolverlas. Para practicar con ejercicios resueltos de este tipo de ecuaciones más complicadas haz clic aquí:
➤ Ver: ejercicios resueltos de ecuaciones de primer grado con paréntesis
Ecuaciones de primer grado con fracciones
Por último, las ecuaciones de primer grado aún se pueden complicar más añadiendo fracciones a la ecuación, ya que si trabajamos con fracciones se deben hacer más cálculos.
Por ejemplo, la siguiente ecuación tiene tres términos con denominadores:
Incluso hay algunas ecuaciones que combinan paréntesis y fracciones en la misma ecuación de primer grado, lo que dificulta aún más su resolución.
Para aprender a resolver ecuaciones de primer grado con fracciones y, además, practicar con ejercicios resueltos, haz clic aquí:
➤ Ver: ejercicios resueltos de ecuaciones de primer grado con fracciones
