▷ Sistemas de ecuaciones

En este artículo se explica qué son los sistemas de ecuaciones lineales y cómo se resuelven. Además, encontrarás ejemplos de sistemas de ecuaciones resueltos con todos los métodos de resolución.

Índice

¿Qué es un sistema de ecuaciones?

Un sistema de ecuaciones es un conjunto de ecuaciones que comparten una solución. Es decir, un sistema de ecuaciones son dos o más ecuaciones que definen una solución.

Cuando el sistema de ecuaciones está formado por ecuaciones de primer grado, se llama sistema de ecuaciones lineales. Asimismo, un sistema de ecuaciones 2×2 es un sistema con dos ecuaciones y dos incógnitas.

Hay cuatro métodos para resolver un sistema de ecuaciones: el método de sustitución, el método de reducción, el método de igualación y el método gráfico. Más abajo veremos cómo resolver un sistema de ecuaciones con cada uno de estos métodos.

Tipos de sistemas de ecuaciones

Los sistemas de ecuaciones lineales se pueden clasificar según el número de sus soluciones:

Sistema Compatible Determinado (SCD): el sistema de ecuaciones tiene una única solución.
Sistema Compatible Indeterminado (SCI): el sistema de ecuaciones tiene infinitas soluciones.
Sistema Incompatible (SI): el sistema de ecuaciones no tiene solución.

Métodos para resolver sistemas de ecuaciones

Una vez hemos visto la definición de sistema de ecuaciones lineales y cuáles son los diferentes tipos de sistemas, vamos a ver cómo se resuelven.

Principalmente, existen cuatro métodos diferentes para resolver un sistema de ecuaciones 2×2:

Método de sustitución
Método de reducción (o método de eliminación)
Método de igualación
Método gráfico

A continuación, se explica cada método de resolución de sistemas de ecuaciones paso a paso.

Método de sustitución

Para resolver un sistema de ecuaciones con el método de sustitución se deben seguir los siguientes pasos:

Despejar una incógnita de una ecuación del sistema.
Sustituir la expresión obtenida en la otra ecuación del sistema.
Hallar el valor de una incógnita resolviendo la ecuación del paso anterior.
Sustituir el valor obtenido en la ecuación del paso 1.
Calcular el valor de la otra incógnita.

Ejemplo de un sistema de ecuaciones resuelto por el método de sustitución

$\left. \begin{array}{l} x + y = 5 \\[2ex] 2x - 2y = 6 \end{array} \right\}$

Lo primero que debemos hacer es despejar una incógnita del sistema de ecuaciones. Puedes despejar cualquier incógnita de cualquier ecuación. En este caso despejaremos la x de la primera ecuación:

$\left. \begin{array}{l} x + y = 5 \\[2ex] 2x - 2y = 6 \end{array} \right\} \left. \begin{array}{l} \longrightarrow \ x = 5-y \\[2ex] & \end{array}$

Truco: es mejor despejar una incógnita que tenga como coeficiente 1 o -1, para así no tener que hacer operaciones con fracciones. Por ejemplo, en este caso el coeficiente de la incógnita x de la primera ecuación es 1, por eso hemos despejado esta incógnita.

En segundo lugar, tenemos que sustituir la expresión obtenida en el paso anterior en la otra ecuación. Es decir, ahora tenemos que sustituir la x de la otra ecuación por la expresión 5-y, ya que x=5-y.

$2x-2y = 6 \quad \xrightarrow{x \ = \ 5-y} \quad 2(5-y)-2y=6$

De esta forma hemos conseguido tener una ecuación de primer grado con una única incógnita, así que la podemos resolver como una ecuación simple. Para ello, eliminamos el paréntesis aplicando la propiedad distributiva:

$2\cdot 5-2\cdot y-2y=6$

$10-2y-2y=6$

Pasamos los términos con incógnita al primer miembro de la ecuación y los términos sin incógnita al otro miembro de la ecuación:

$-2y -2y = -10 +6$

Sumamos y restamos los términos de cada lado:

$-4y = -4$

Y despejamos la incógnita y:

$y = \cfrac{-4}{-4}$

$y=1$

Una vez conocemos el valor de la incógnita y, debemos sustituir dicho valor en la expresión donde hemos despejado la incógnita x:

$x = 5-y \quad \xrightarrow{y \ = \ 1} \quad x=5-1$

Y, finalmente, calculamos el valor numérico de la incógnita x:

$x=5-1=4$

Por lo tanto, la solución de sistema de ecuaciones lineales es:

$\bm{x = 4\qquad y=1}$

Aunque no es necesario hacerlo, se puede comprobar que el sistema de ecuaciones está bien resuelto sustituyendo la solución obtenida en el sistema de ecuaciones original:

$\left. \begin{array}{l}x+y=5\\[2ex]2x-2y=6\end{array} \right\} \xrightarrow{x=4 \ y=1} \left. \begin{array}{l}4+1=5\\[2ex] 2\cdot 4-2\cdot1=6\end{array} \right\} \left. \begin{array}{l} 5=5\\[2ex]6=6\end{array} \right\}$

Hemos obtenido una igualdad en las dos ecuaciones del sistema, por lo que la solución es correcta. ✅

➤ Ver: ejercicios resueltos por el método de sustitución

Método de reducción

Para resolver un sistema de ecuaciones por el método de reducción (o método de eliminación) se deben seguir los siguientes pasos:

Operar con las ecuaciones del sistema para que los coeficientes de una incógnita tengan el mismo valor pero de signo contrario.
Sumar las ecuaciones del sistema.
Resolver la ecuación resultante.
Sustituir el valor obtenido en una de las ecuaciones iniciales.
Resolver la ecuación y hallar el valor de la otra incógnita.

Ejemplo de un sistema de ecuaciones resuelto por el método de reducción

$\left. \begin{array}{l} -5x +6y = 7\\[2ex] 4x +3y = 10\vphantom{\xrightarrow{\times(-2)}}\end{array} \right\}$

En primer lugar, tenemos que hacer operaciones con las ecuaciones de manera que los coeficientes de una incógnita sean iguales pero de signo contrario. En este caso, el coeficiente de la incógnita y de la primera ecuación es el doble que el de la segunda ecuación, por tanto, basta con multiplicar la segunda ecuación por -2:

$\left. \begin{array}{l} -5x +6y = 7\\[2ex] 4x +3y = 10 \vphantom{\xrightarrow{\times(-2)}}\end{array} \right\}\begin{array}{l} \\[2ex] \xrightarrow{\times (-2)} \ -8x -6y =- 20 \end{array}$

Una vez hemos transformado las ecuaciones del sistema, tenemos que sumarlas:

$\begin{array}{crrcr} &-5x&+6y&=&7 \\ +&-8x&-6y&=&-20 \\ \hline &-13x&&=&-13\end{array} \right\}$

De esta forma hemos podido eliminar una incógnita del sistema y simplemente nos queda una ecuación de primer grado que podemos resolver fácilmente:

$-13x=-13$

$x= \cfrac{-13}{-13}$

$x=1$

Ahora que ya sabemos el valor de una incógnita, sustituimos dicho valor en cualquier ecuación del principio para calcular la otra incógnita.

$-5x +6y = 7 \quad \xrightarrow{x \ = \ 1} \quad -5\cdot 1+6y =7$

$-5+6y =7$

$6y = 5 +7$

$6y = 12$

$y= \cfrac{12}{6}$

$y=2$

En conclusión, la solución del sistema de ecuaciones es:

$\bm{x=1\qquad y=2}$

➤ Ver: ejercicios resueltos por el método de reducción

Método de igualación

Para resolver un sistema de ecuaciones por el método de igualación se deben hacer los siguientes pasos:

Despejar la misma incógnita de las dos ecuaciones del sistema.
Igualar las dos expresiones obtenidas.
Resolver la ecuación con una sola incógnita resultante.
Sustituir el valor obtenido en cualquier ecuación inicial.
Resolver dicha ecuación y hallar el valor de la otra incógnita.

Ejemplo de un sistema de ecuaciones resuelto por el método de igualación

$\left. \begin{array}{l} 3x + 2y = 7 \\[4ex] 2x -3y = 9 \end{array} \right\}$

Lo primero que debemos hacer es despejar la misma incógnita de las dos ecuaciones. Puedes despejar la incógnita que quieras, pero siempre la misma en las dos ecuaciones. En este caso despejaremos la incógnita x:

$\left. \begin{array}{l} 3x + 2y = 7 \vphantom{\cfrac{7-2y}{3}} \\[3ex] 2x -3y = 9 \vphantom{\cfrac{7-2y}{3}} \end{array} \right\} \left. \begin{array}{l}\longrightarrow \ 3x = 7-2y \ \longrightarrow \ x = \cfrac{7-2y}{3} \\[3ex] \longrightarrow \ 2x = 9+3y \ \longrightarrow \ x= \cfrac{9+3y}{2} \end{array}$

Una vez hemos despejado la misma incógnita de cada ecuación que forma el sistema, igualamos las dos expresiones obtenidas:

$x=x$

$\cfrac{7-2y}{3} = \cfrac{9+3y}{2}$

Y resolvemos la ecuación obtenida. En este caso se trata de una ecuación de primer grado con fracciones, por lo tanto, primero debemos multiplicar cada término de la ecuación por el mínimo común múltiplo (mcm) de los denominadores para eliminar las fracciones:

$6\cdot\cfrac{7-2y}{3} = 6\cdot\cfrac{9+3y}{2}$

$2\cdot (7-2y) = 3\cdot (9+3y)$

Aplicamos la propiedad distributiva para quitar los paréntesis:

$14-4y = 27 + 9y$

Y despejamos la incógnita:

$-4y -9y = -14+27$

$-13y=13$

$y= \cfrac{13}{-13}$

$y =-1$

Ahora que ya conocemos el valor de una incógnita, sustituimos dicho valor en cualquier ecuación del principio para calcular el valor de la otra incógnita:

$3x + 2y = 7 \quad \xrightarrow{y \ = \ -1} \quad 3x + 2\cdot (-1)=7$

$3x-2=7$

$3x=7+2$

$3x=9$

$x= \cfrac{9}{3}$

$x=3$

En resumen, la solución del sistema de ecuaciones es:

$\bm{x=3\qquad y=-1}$

➤ Ver: ejercicios resueltos por el método de igualación

Método gráfico

Para resolver un sistema de ecuaciones por el método gráfico se deben hacer los siguientes pasos:

Despejar la incógnita y de las dos ecuaciones del sistema.
Construir una tabla de valores para cada ecuación.
Representar gráficamente las dos ecuaciones en el plano cartesiano. Se obtendrán dos rectas:
- Si las dos rectas se cortan en un punto, dicho punto de corte es la solución del sistema de ecuaciones (Sistema Compatible Determinado).
- Si las dos rectas se superponen, el sistema de ecuaciones tiene infinitas soluciones (Sistema Compatible Indeterminado).
- Si las dos rectas son paralelas (no se cortan), el sistema de ecuaciones no tiene solución (Sistema Incompatible).

Ejemplo de un sistema de ecuaciones resuelto por el método gráfico

$\left.\begin{array}{l}2x+y=5\\[2ex] -3x +2y = -4 \end{array}\right\}$

En primer lugar, tenemos que despejar la incógnita y de las dos ecuaciones que forman el sistema:

$\left.\begin{array}{l}2x+y=5\\[2ex] \displaystyle \vphantom{\frac{3x-4x}{2}} -3x +2y = -4 \end{array}\right\}\begin{array}{l}\longrightarrow \ y=-2x+5\\[2ex]\displaystyle \longrightarrow \ 2y=3x-4 \ \longrightarrow \ y=\frac{3x-4}{2} \end{array}$

Una vez tenemos despejada la y de ambas ecuaciones, debemos hacer una tabla de valores para cada ecuación. Y para construir una tabla de valores simplemente tenemos que otorgar valores (los que quieras) a la incógnita x, hacer los cálculos que se indican en cada ecuación, y el valor obtenido será la coordenada y correspondiente a ese punto.

Entonces, creamos la tabla de valores para la primera ecuación:

$y=-2x+5$

$x= 0 \ \longrightarrow \ y = -2\cdot 0+5=5}$

$x= 1 \ \longrightarrow \ y = -2\cdot 1+5= 3$

$\begin{array}{c|c} x & y \\ \hline 0 & 5 \\ 1 & 3 \end{array}$

Una vez hemos calculado la tabla de valores de una ecuación, debemos representar los puntos obtenidos en un gráfico. Recuerda que la primera coordenada de un punto, la coordenada x, corresponde al eje horizontal, y la segunda coordenada de un punto, la coordenada y, corresponde al eje vertical.

$y=-2x+5$

$\begin{array}{c|c} x & y \\ \hline 0 & 5 \\ 1 & 3 \end{array}$

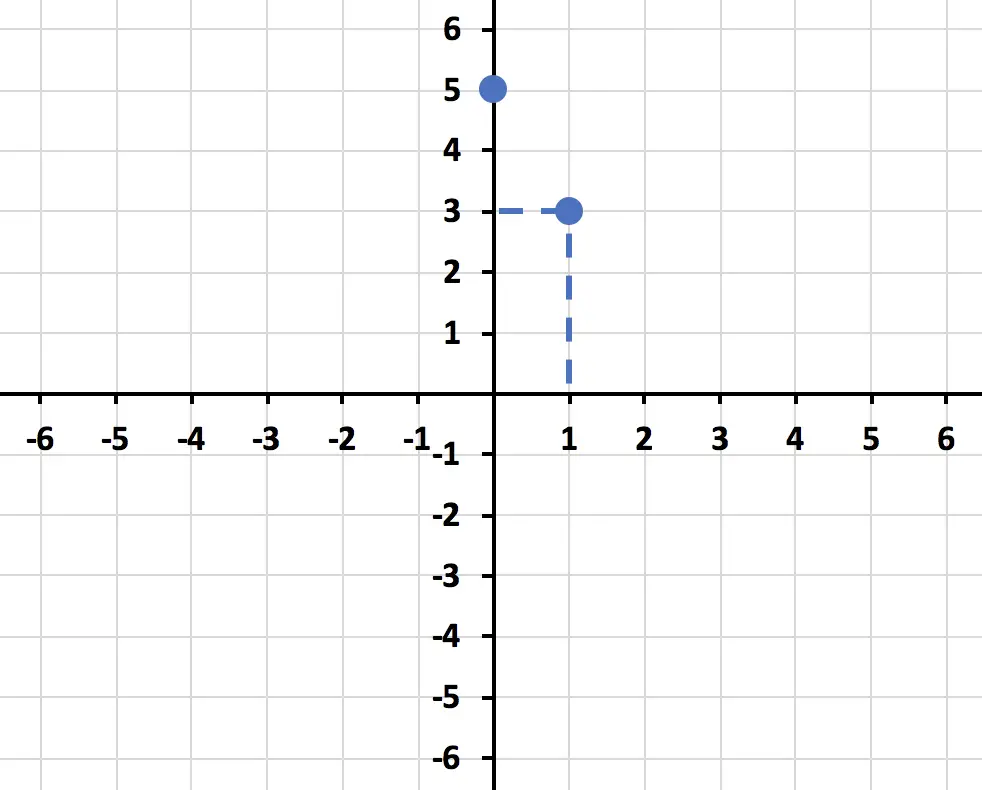
Y unimos los puntos representados para formar una recta:

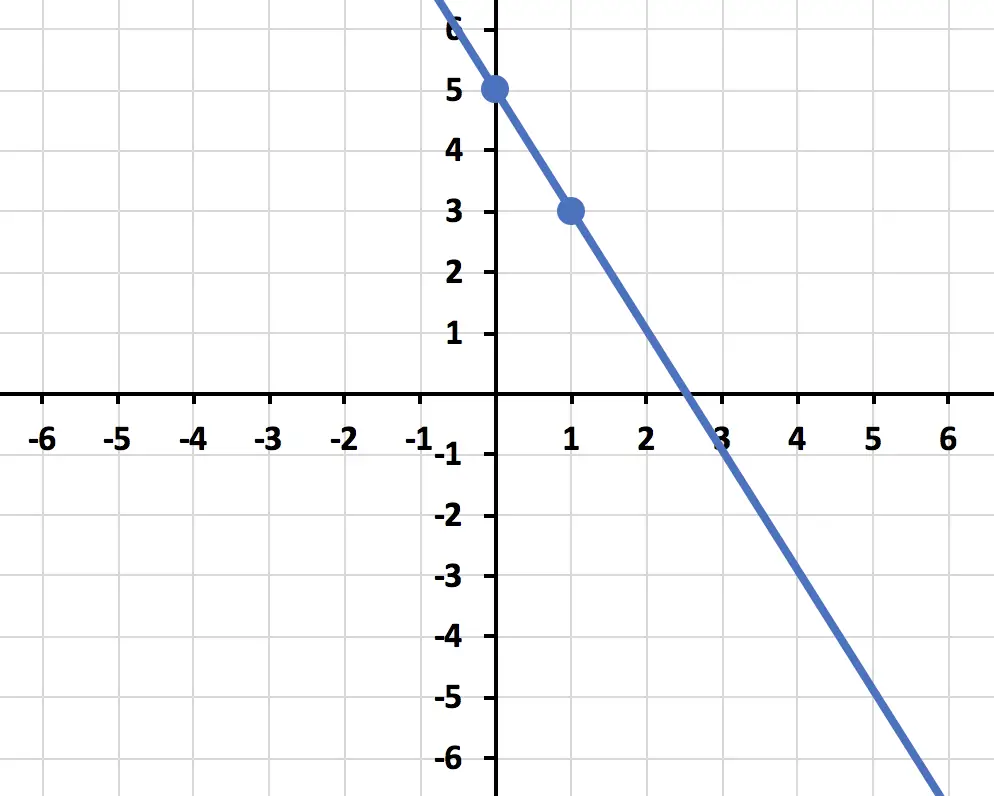
como representar una recta en un grafico

Aunque calculando dos puntos por cada ecuación es suficiente, si quieres puedes calcular algún otro punto para comprobar que la recta está bien representada.

Ahora debemos repetir el mismo proceso con la otra ecuación del sistema. Así pues, construimos la tabla de valores de la segunda ecuación:

$y=\cfrac{3x-4}{2}$

$x= 0 \ \longrightarrow \ y=\cfrac{3\cdot 0-4}{2}=-2$

$x= 2 \ \longrightarrow \ y=\cfrac{3\cdot 2-4}{2}=1$

$\begin{array}{c|c} x & y \\ \hline 0 & -2 \\ 2 & 1 \end{array}$

Cuando ya tenemos la tabla de valores, representamos los puntos obtenidos en el mismo gráfico que hemos representado la recta anterior:

$y=\cfrac{3x-4}{2}$

$\begin{array}{c|c} x & y \\ \hline 0 & -2 \\ 2 & 1 \end{array}$

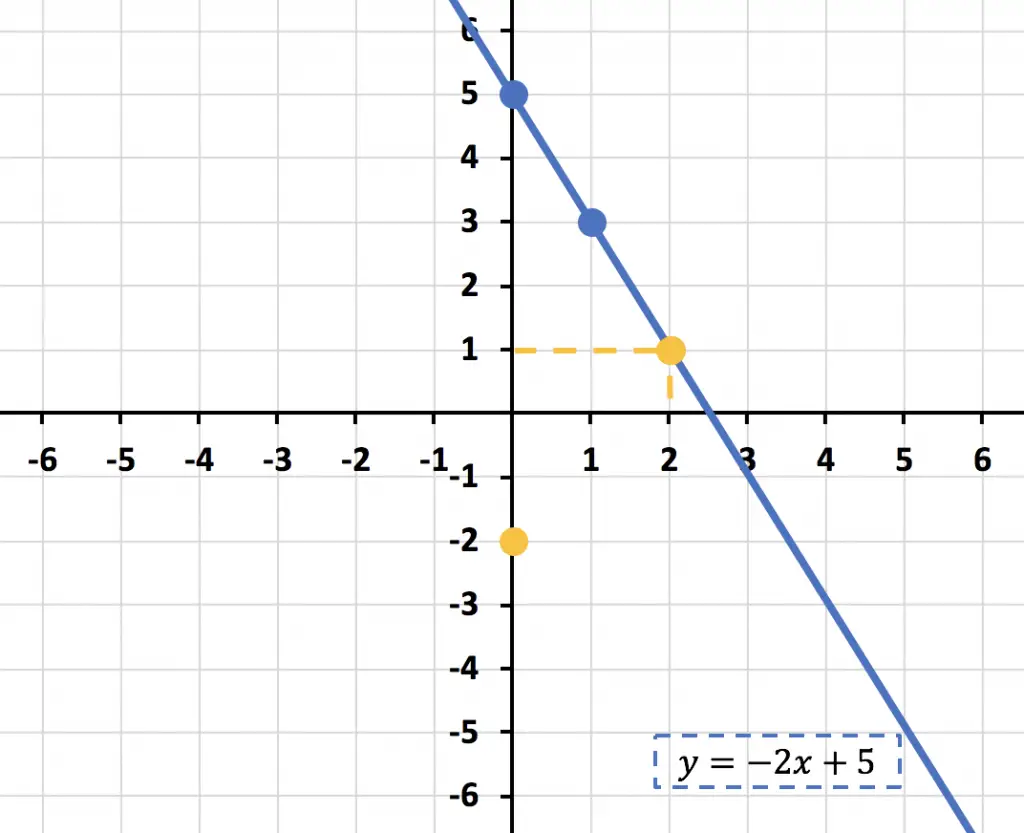
como representar las ecuaciones de un sistema en un grafico

Y unimos los puntos para formar la otra recta:

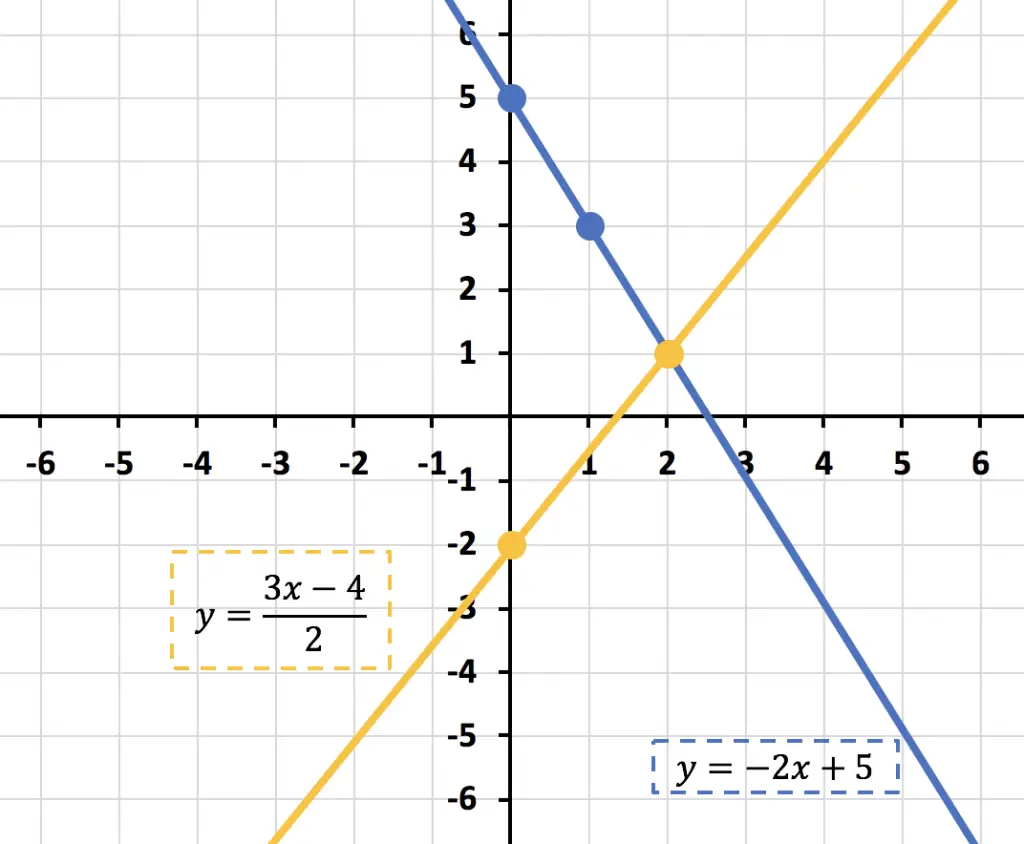
como representar un sistema de ecuaciones en un grafico

Una vez hemos representado las dos ecuaciones en un gráfico, ya podemos saber cuál es la solución del sistema de ecuaciones. La solución del sistema de ecuaciones es el punto donde se cortan las dos rectas, que en este caso es el punto (2,1):

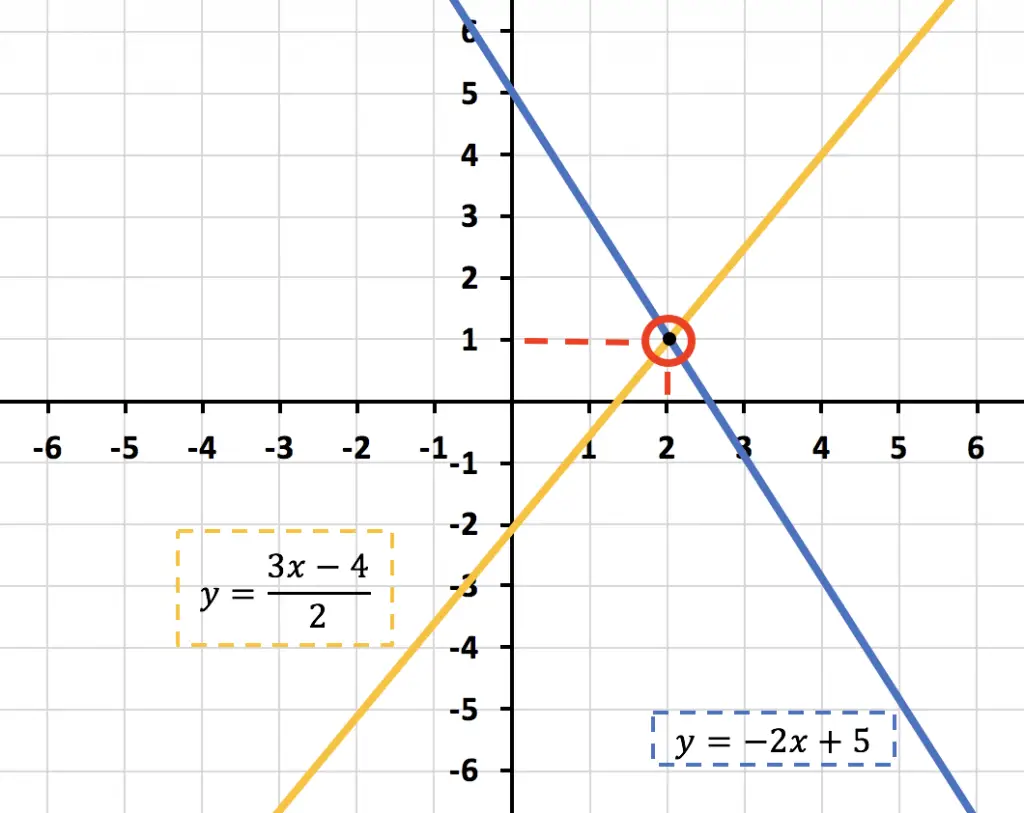
Como las rectas solamente se cruzan en el punto (2,1) la única solución del sistema de ecuaciones es:

$\bm{x = 2 \qquad y = 1}$

En este caso, el sistema tiene una sola solución, por lo que se trata de un Sistema Compatible Determinado (SCD). Sin embargo, ten en cuenta que si las dos rectas estuvieran representadas una encima de la otra, el sistema tendría infinitas soluciones y por tanto sería un Sistema Compatible Indeterminado (SCI). Por otro lado, si las dos rectas fueran paralelas, el sistema no tendría ninguna solución y por tanto sería un Sistema Incompatible (SI).

➤ Ver: ejercicios resueltos por el método gráfico

Sistema de ecuaciones