▷ Ecuaciones de segundo grado (o ecuaciones cuadráticas)

En este post se explica qué es una ecuación de segundo grado (o ecuación cuadrática) y cómo se resuelve. Así pues, encontrarás la fórmula general de las ecuaciones de segundo grado y, además, ejercicios resueltos paso a paso para practicar.

Índice

¿Qué son las ecuaciones de segundo grado?

Las ecuaciones de segundo grado, también llamadas ecuaciones cuadráticas, son ecuaciones en las que la incógnita (normalmente x) está elevada a la 2. Por lo tanto, las ecuaciones de segundo grado son de la forma ax²+bx+c=0.

Para resolver una ecuación de segundo grado se debe utilizar la fórmula general. Además, las ecuaciones de segundo grado tienen como máximo dos soluciones.

Fórmula general de las ecuaciones de segundo grado

La fórmula general de las ecuaciones de segundo grado es la siguiente:

formula general de las ecuaciones de segundo grado o ecuaciones cuadraticas

De modo que la fórmula general sirve para resolver cualquier tipo de ecuación de segundo grado. Para utilizar la fórmula simplemente tienes que identificar cada término de la ecuación de segundo grado y sustituirlo donde corresponda en la fórmula general.

Ejemplo de una ecuación de segundo grado resuelta

Para que veas cómo se hacen las ecuaciones de segundo grado, a continuación tienes resuelta paso a paso una ecuación de este tipo a modo de ejemplo.

$x^2+2x-3=0$

Para resolver una ecuación de segundo grado, debemos usar la fórmula general que hemos visto más arriba:

$\displaystyle x=\frac{-b\pm \sqrt{ b^2-4\cdot a \cdot c}}{2\cdot a}$

Por lo tanto, lo primero que debemos hacer es identificar los parámetros a, b y c de la ecuación de segundo grado. El parámetro a es el coeficiente del término de segundo grado, que en este caso es 1, el parámetro b es el número que acompaña la x, que es 2, y el parámetro c es el término sin incógnita, que es -3.

$\begin{array}{c}x^2+2x-3=0\\[3ex]ax^2+bx+c=0\end{array}\ \color{orange} \bm{\longrightarrow}\color{black}\begin{array}{c}a=1\\[2ex]b=2\\[2ex]c=-3\end{array}$

Fíjate que debes tomar los números junto con sus signos para aplicar correctamente la fórmula general.

Una vez hemos identificado los parámetros de la ecuación cuadrática, empleamos la fórmula general. Así pues, sustituimos cada parámetro por su valor en la fórmula:

$\displaystyle x=\frac{-b\pm \sqrt{ b^2-4\cdot a \cdot c}}{2\cdot a}\color{orange} \ \bm{\longrightarrow}\color{black} \ x=\frac{-2\pm \sqrt{ 2^2-4\cdot 1 \cdot (-3)}}{2\cdot 1}$

Ahora hacemos los cálculos:

$\displaystyle x=\frac{-2\pm \sqrt{4+12}}{2}$

$\displaystyle x=\frac{-2\pm \sqrt{16}}{2}$

Si te fijas en la fórmula, delante de la raíz hay el signo más junto con el signo menos, eso es debido a que las raíces cuadradas pueden tener dos soluciones: una positiva y otra negativa. En consecuencia, tenemos que hacer el cálculo por cada posible solución de la raíz:

$\displaystyle x=\frac{-2\pm 4}{2}=\begin{cases}\displaystyle\frac{-2+4}{2}=\frac{2}{2}=1\\[4ex]\displaystyle\frac{-2-4}{2}=\frac{-6}{2}=-3\end{cases}$

En conclusión, las dos soluciones de la ecuación de segundo grado son:

$\bm{x=1}\qquad\bm{x=-3}$

Ejercicios resueltos de ecuaciones de segundo grado

Ejercicio 1

Resuelve la siguiente ecuación de segundo grado completa:

$x^2-3x+2=0$

Ver solución

Se trata de una ecuación de segundo grado, por lo que tenemos que usar la fórmula general para resolverla:

$\displaystyle x=\frac{-b\pm \sqrt{ b^2-4\cdot a \cdot c}}{2\cdot a}$

Así pues, identificamos el valor de cada parámetro:

$\begin{array}{c}x^2-3x+2=0\\[3ex]ax^2+bx+c=0\end{array}\ \color{orange} \bm{\longrightarrow}\color{black}\begin{array}{c}a=1\\[2ex]b=-3\\[2ex]c=2\end{array}$

Ahora sustituimos el valor de cada parámetro en la fórmula general:

$\displaystyle x=\frac{-(-3)\pm \sqrt{(-3)^2-4\cdot 1 \cdot 2}}{2\cdot 1}$

Y hacemos los cálculos para hallar las dos soluciones de la ecuación de segundo grado:

$\begin{array}{l}\displaystyle x=\frac{3\pm \sqrt{9-8}}{2}\\[3ex]\displaystyle x=\frac{3\pm \sqrt{1}}{2}\\[3ex]\displaystyle x=\frac{3\pm 1}{2}=\begin{cases}\displaystyle\frac{3+1}{2}=\frac{4}{2}=2\\[4ex]\displaystyle\frac{3-1}{2}=\frac{2}{2}=1\end{cases}\end{array}$

Ejercicio 2

Calcula las soluciones de la siguiente ecuación de segundo grado:

$x^2+6x+8=0$

Ver solución

Para determinar las soluciones de la ecuación de segundo grado, tenemos que aplicar la fórmula general de este tipo de ecuaciones:

$\displaystyle x=\frac{-b\pm \sqrt{ b^2-4\cdot a \cdot c}}{2\cdot a}$

De modo que primero debemos averiguar el valor de cada parámetro de la fórmula:

$\begin{array}{c}x^2+6x+8=0\\[3ex]ax^2+bx+c=0\end{array}\ \color{orange} \bm{\longrightarrow}\color{black}\begin{array}{c}a=1\\[2ex]b=6\\[2ex]c=8\end{array}$

Luego sustituimos el valor de cada parámetro en la fórmula de las ecuaciones de segundo grado:

$\displaystyle x=\frac{-6\pm \sqrt{6^2-4\cdot 1 \cdot 8}}{2\cdot 1}$

Por último, calculamos las operaciones resultantes para obtener las dos soluciones de la ecuación cuadrática:

$\begin{array}{l}\displaystyle x=\frac{-6\pm \sqrt{36-32}}{2}\\[3ex]\displaystyle x=\frac{-6\pm \sqrt{4}}{2}\\[3ex]\displaystyle x=\frac{-6\pm 2}{2}=\begin{cases}\displaystyle\frac{-6+2}{2}=\frac{-4}{2}=-2\\[4ex]\displaystyle\frac{-6-2}{2}=\frac{-8}{2}=-4\end{cases}\end{array}$

Ejercicio 3

Resuelve la siguiente ecuación cuadrática completa:

$2x^2+5x+6=0$

Ver solución

La fórmula general para resolver ecuaciones cuadráticas completas es la siguiente:

$\displaystyle x=\frac{-b\pm \sqrt{ b^2-4\cdot a \cdot c}}{2\cdot a}$

Así pues, el parámetro a es el coeficiente del término cuadrático, el parámetro b es el coeficiente del término lineal y el parámetro c es el término independiente de la ecuación:

$\begin{array}{c}2x^2+5x+6=0\\[3ex]ax^2+bx+c=0\end{array}\ \color{orange} \bm{\longrightarrow}\color{black}\begin{array}{c}a=2\\[2ex]b=5\\[2ex]c=6\end{array}$

Sustituimos el valor de cada parámetro en la fórmula general:

$\displaystyle x=\frac{-5\pm \sqrt{5^2-4\cdot 2 \cdot 6}}{2\cdot 2}$

Hacemos los cálculos:

$\begin{array}{l}\displaystyle x=\frac{-5\pm \sqrt{25-48}}{4}\\[3ex]\displaystyle x=\frac{-5\pm \sqrt{-24}\color{red}\bm{\times}\color{black}}{4} \ \end{array}$

Sin embargo, las raíces cuadradas de números negativos no tienen ninguna solución real, por lo tanto, la ecuación de segundo grado tampoco tiene ninguna solución real.

Ejercicio 4

Encuentra las soluciones de la siguiente ecuación cuadrática:

$\displaystyle 10x^2+3x-1=0$

Ver solución

La fórmula general de las ecuaciones cuadráticas es la siguiente:

$\displaystyle x=\frac{-b\pm \sqrt{ b^2-4\cdot a \cdot c}}{2\cdot a}$

Así pues, identificamos cuánto vale cada parámetro de la fórmula:

$\begin{array}{c}10x^2+3x-1=0\\[3ex]ax^2+bx+c=0\end{array}\ \color{orange} \bm{\longrightarrow}\color{black}\begin{array}{c}a=10\\[2ex]b=3\\[2ex]c=-1\end{array}$

Sustituimos el valor de cada parámetro en la fórmula:

$\displaystyle x=\frac{-3\pm \sqrt{3^2-4\cdot 10 \cdot (-1)}}{2\cdot 10}$

Por último, hacemos los cálculos para encontrar las dos soluciones de la ecuación cuadrática:

$\begin{array}{l}\displaystyle x=\frac{-3\pm \sqrt{9+40}}{20}\\[3ex]\displaystyle x=\frac{-3\pm \sqrt{49}}{20}\\[3ex]\displaystyle x=\frac{-3\pm 7}{20}=\begin{cases}\displaystyle\frac{-3+7}{20}=\frac{4}{20}=\frac{1}{5}\\[4ex]\displaystyle\frac{-3-7}{20}=\frac{-10}{20}=-\frac{1}{2}\end{cases}\end{array}$

Ejercicio 5

Halla las soluciones de la siguiente ecuación de segundo grado:

$3x^2+2x-15+x=2x^2+4x-3$

Ver solución

Antes de utilizar la fórmula general, tenemos que simplificar los términos. Así que pasamos todos los términos al mismo miembro de la ecuación:

$3x^2-2x^2+2x+x-4x-15+3=0$

Y ahora sumamos los términos que tienen el mismo grado:

$x^2-x-12=0$

De este forma, una vez ya tenemos la ecuación simplificada, ya podemos emplear la fórmula general:

$\displaystyle x=\frac{-b\pm \sqrt{ b^2-4\cdot a \cdot c}}{2\cdot a}$

El valor de cada parámetro de la fórmula es el siguiente:

$\begin{array}{c}x^2-x-12=0\\[3ex]ax^2+bx+c=0\end{array}\ \color{orange} \bm{\longrightarrow}\color{black}\begin{array}{c}a=1\\[2ex]b=-1\\[2ex]c=-12\end{array}$

Sustituimos el valor de cada parámetro en la fórmula:

$\displaystyle x=\frac{-(-1)\pm \sqrt{(-1)^2-4\cdot 1 \cdot (-12)}}{2\cdot 1}$

Y, finalmente, calculamos las dos soluciones de la ecuación de segundo grado:

$\begin{array}{l}\displaystyle x=\frac{1\pm \sqrt{1+48}}{2}\\[3ex]\displaystyle x=\frac{1\pm \sqrt{49}}{2}\\[3ex]\displaystyle x=\frac{1\pm 7}{2}=\begin{cases}\displaystyle\frac{1+7}{2}=\frac{8}{2}=4\\[4ex]\displaystyle\frac{1-7}{2}=\frac{-6}{2}=-3\end{cases}\end{array}$

Puedes practicar con ejercicios resueltos de ecuaciones de segundo grado más difíciles en los siguientes enlaces:

➤ Ver: ejercicios resueltos de ecuaciones de segundo grado con paréntesis
➤ Ver: ejercicios resueltos de ecuaciones de segundo grado con fracciones

Número de soluciones de una ecuación de segundo grado

Ahora que ya has visto cómo calcular las soluciones de una ecuación de segundo grado, debes saber que se puede saber el número de soluciones que tiene una ecuación de segundo grado sin necesidad de calcularlas.

Calculando el discriminante de una ecuación de segundo grado se puede determinar cuántas soluciones tiene. Así pues, la fórmula del discriminante es la siguiente.

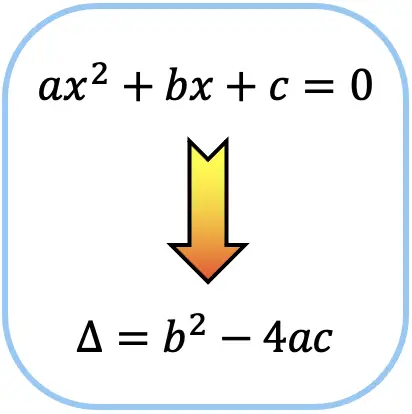
numero de soluciones que tiene una ecuacion de segundo grado

El signo del discriminante (Δ=b²-4ac) determina el número de soluciones de una ecuación de segundo grado:

Si el discriminante es positivo (Δ>0), la ecuación de segundo grado tiene dos soluciones diferentes.
Si el discriminante es nulo (Δ=0), la ecuación de segundo grado tiene dos soluciones iguales.
Si el discriminante es negativo (Δ<0), la ecuación de segundo grado no tiene ninguna solución real.

Para acabar de entender este concepto matemático, vamos a hallar el número de soluciones (o raíces) de la siguiente ecuación cuadrática:

$x^2+5x+4 = 0$

Para averiguar el número de soluciones de la ecuación de grado 2 tenemos que calcular el discriminante, cuya fórmula es:

$\Delta = b^2-4ac$

De manera que para hallar el discriminante simplemente debemos sustituir las variables de la fórmula por sus valores correspondientes: $a$ es el coeficiente del término cuadrático que en este caso es 1, $b$ es el término que acompaña al término de primer grado que es 5, y $c$ es el término independiente, esto es, 4.

$\begin{aligned} \Delta & = 5^2-4\cdot 1\cdot 4 \\[1.5ex] & = 25 -16 \\[1.5ex] & = 9 \color{orange} \end{aligned}$

El discriminante de la ecuación de segundo grado es positivo, por lo tanto, la ecuación posee 2 soluciones distintas.

Ecuaciones de segundo grado incompletas

A lo largo del artículo se ha explicado cómo resolver las ecuaciones de segundo grado completas. Sin embargo, debes saber que también existen las ecuaciones de segundo grado incompletas, lo que significa que les falta algún término:

Ecuaciones de segundo grado incompleta con ausencia de b, es decir, sin término lineal:

$ax^2+c=0$

Ecuaciones de segundo grado incompleta con ausencia de c, esto es, sin término independiente:

$ax^2+bx=0$

Ecuaciones de segundo grado incompleta con ausencia de b y de c:

$ax^2=0$

Así pues, cada tipo de ecuación de segundo grado incompleta se resuelve de una manera diferente. Haz clic en el siguiente enlace para ver la explicación de cada método y practicar con ejercicios resueltos de cada tipo de ecuación cuadrática incompleta:

➤ Ver: ecuaciones de segundo grado incompletas

¿Qué son las ecuaciones de segundo grado?

Fórmula general de las ecuaciones de segundo grado

Ejemplo de una ecuación de segundo grado resuelta

Ejercicios resueltos de ecuaciones de segundo grado

Ejercicio 1

Ejercicio 2

Ejercicio 3

Ejercicio 4

Ejercicio 5

Número de soluciones de una ecuación de segundo grado

Ecuaciones de segundo grado incompletas

Deja un comentario Cancelar respuesta