▷ Tipos de sistemas de ecuaciones

En esta página te explicamos cuáles son todos los tipos de sistemas de ecuaciones lineales (SCD, SCI, SI) según el números de sus soluciones y, además, cómo se puede determinar qué tipo de sistema es de manera fácil (sin resolver el sistema).

Índice

¿Cuáles son los tipos de sistemas de ecuaciones lineales?

Los sistemas de ecuaciones lineales se pueden clasificar según el número de sus soluciones:

Si un sistema tiene una única solución, es un sistema compatible determinado (SCD).
Si un sistema tiene infinitas soluciones, es un sistema compatible indeterminado (SCI).
Si un sistema no tiene solución, es un sistema incompatible (SI).

Cada tipo de sistema de ecuación tiene sus propiedades, así que a continuación vamos a analizarlos uno a uno.

Sistema compatible determinado

Un sistema compatible determinado posee una sola solución. Además, si se representan en un gráfico las ecuaciones de un sistema compatible determinado, estas se cortan en 1 único punto que es la solución del sistema.

Por ejemplo, el siguiente sistema de ecuaciones lineales es compatible determinado porque tiene una solución:

$\left. \begin{array}{l} -2x+y=-4 \\[2ex] 2x+3y=12 \end{array} \right\} \color{orange}\bm{\longrightarrow}\color{black} \begin{array}{c} x=3 \\[1.5ex] y=2 \end{array}$

Recuerda que existen 4 métodos para resolver un sistema de ecuaciones: método de sustitución, de reducción, de igualación y gráfico.

Pues al representar gráficamente las dos ecuaciones que forman el sistema, obtenemos dos rectas que se intersecan precisamente en el punto (3,2), cuyas coordenadas son la solución del sistema.

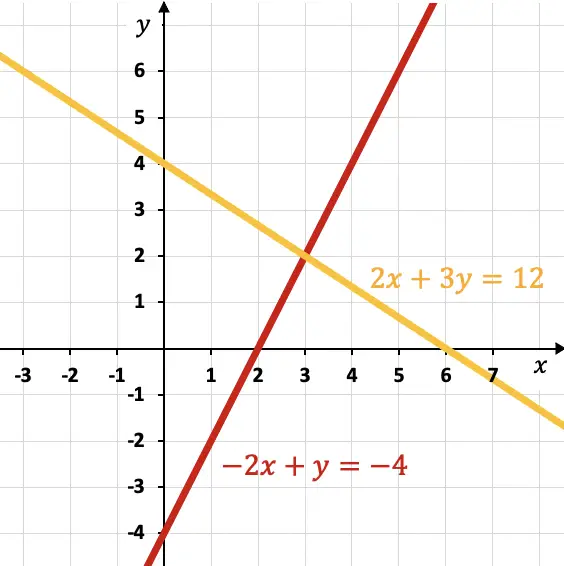
soluciones de un sistema de ecuaciones compatible determinado

Sistema compatible indeterminado

Un sistema compatible indeterminado tiene infinitas soluciones. Esto significa que las ecuaciones de un sistema compatible indeterminado se cumplen por cualquier valor que tomen las incógnitas.

Por otro lado, la representación gráfica de un sistema de ecuaciones compatible indeterminado corresponde a dos rectas coincidentes, es decir, una recta se superpone encima de la otra.

A modo de ejemplo, vamos a solucionar el siguiente sistema de ecuaciones lineales, que es del tipo compatible indeterminado:

$\left. \begin{array}{l} 3x-2y=8 \\[2ex] 6x-4y=16 \end{array} \right\}$

En este ejercicio utilizaremos el método de reducción ya que las dos ecuaciones son proporcionales. Así que primero multiplicamos la primera ecuación por -2:

$3x-2y=8 \ \xrightarrow{\times (-2)} \ -6x+4y=-16$

Y luego sumamos las dos ecuaciones del sistema:

$\begin{array}{r} -6x+4y =-16 \\[1.2ex] 6x-4y = \phantom{-}16 \\ \hline \vphantom{\sqrt{x^2}} 0 = \phantom{-1}0 \end{array}$

Sin embargo, obtenemos una igualdad en la que no aparece ninguna incógnita, por lo tanto, siempre se cumplirá por cualquier valor que tomen las variables. De forma que el sistema de ecuaciones lineales tiene infinitas soluciones y, en consecuencia, se trata de un sistema compatible indeterminado.

Por último, también se puede analizar la compatibilidad del sistema representando gráficamente las dos ecuaciones:

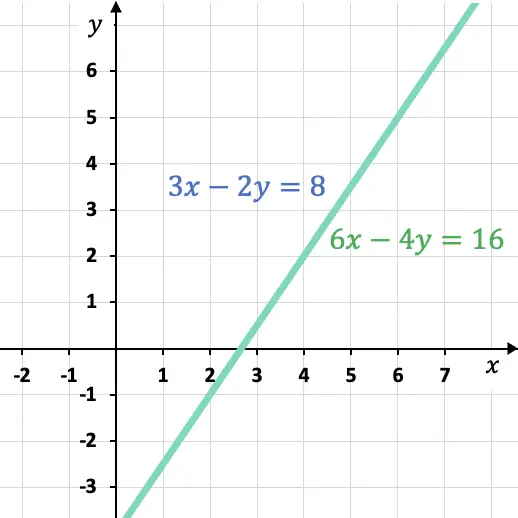
soluciones infinitas de una sistema de ecuaciones compatible indeterminado

Como puedes comprobar, las dos rectas son coincidentes (están superpuestas) en la gráfica, de manera que se trata de un sistema de ecuaciones compatible indeterminado.

Sistema incompatible

Un sistema de ecuaciones incompatible no tiene ninguna solución posible. Aparte, también se puede distinguir un sistema incompatible representando las ecuaciones en una gráfica, ya que las rectas de este tipo de sistema de ecuaciones son paralelas (nunca se cortan).

Para que veas cómo son estos tipos de sistemas, hemos resuelto un ejemplo a continuación:

$\left. \begin{array}{l} -2x+y=3 \\[2ex] -4x+2y=-2 \end{array} \right\}$

Resolveremos el sistema de ecuaciones mediante el método de sustitución, por lo que despejamos la incógnita y de la primera ecuación:

$\left.\begin{array}{l} -2x+y=3 \\[2ex] -4x+2y=-2 \end{array} \right\}\begin{array}{l} \longrightarrow \ y =3+2x \\[2ex] & \end{array}$

Ahora sustituimos la expresión algebraica obtenida en la otra ecuación:

$-4x+2y=-2 \ \xrightarrow{ y \ = \ 3+2x} \ -4x+2(3+2x)=-2$

Y hallamos el valor de la incógnita x:

$-4x+2(3+2x)=-2$

$-4x+6+4x=-2$

$-4x+4x=-2-6$

$0=-8$

Pero la igualdad que hemos obtenido nunca se cumplirá, porque 0 nunca será igual a -8. De modo que el sistema de ecuaciones lineales no se puede resolver y, por lo tanto, consiste en un sistema incompatible.

Por otra parte, también se puede demostrar la incompatibilidad del sistema representando gráficamente las dos ecuaciones:

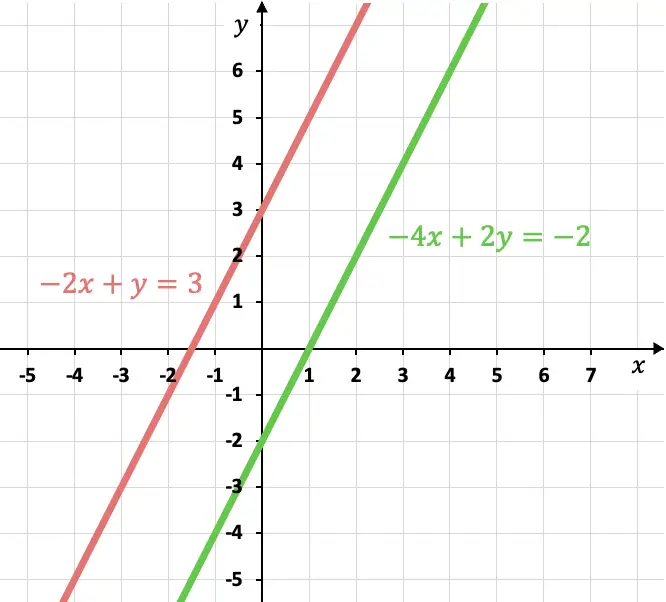
sistema de ecuaciones incompatible sin soluciones

Como puedes ver, las dos rectas representadas en la gráfica son paralelas, así que el sistema es incompatible y no tiene ninguna solución.

¿Cómo saber qué tipo de sistema de ecuaciones es?

Acabamos de ver cómo es cada tipo de sistema de ecuaciones y cómo son las soluciones de cada uno. Sin embargo, existe una manera de averiguar qué tipo de sistema de ecuaciones se trata sin necesidad de resolverlo.

Se pueden identificar los diferentes tipos de sistemas de ecuaciones lineales a partir de la proporcionalidad de sus coeficientes:

Cuando los coeficientes de las incógnitas no son proporcionales, se trata de un sistema compatible determinado.

$\left. \begin{array}{l} 4x-3y=2 \\[2ex] x+2y=7 \end{array} \right\} \color{orange}\bm{\longrightarrow}\color{black} \cfrac{4}{1} \neq \cfrac{-3}{2}\color{orange}\bm{\longrightarrow}\color{black} \text{SCD}$

Cuando todos los coeficientes de las incógnitas son proporcionales entre sí, corresponde a un sistema compatible indeterminado.

$\left. \begin{array}{l} 4x+2y=10\\[2ex] 2x+y=5 \end{array} \right\} \color{orange}\bm{\longrightarrow}\color{black} \cfrac{4}{2}= \cfrac{2}{1}=\cfrac{10}{5} \color{orange}\bm{\longrightarrow}\color{black} \text{SCI}$

Cuando los coeficientes de las incógnitas son proporcionales entre sí pero no con los términos independientes, consiste en un sistema incompatible.

$\left. \begin{array}{l} 3x-4y=2\\[2ex] 6x-8y=9 \end{array} \right\} \color{orange}\bm{\longrightarrow}\color{black} \cfrac{3}{6}= \cfrac{-4}{-8}\neq \cfrac{2}{9} \color{orange}\bm{\longrightarrow}\color{black} \text{SI}$

De esta manera, podemos distinguir qué tipo de sistema de ecuaciones es mucho más rápidamente, porque no hace falta resolver el sistema.

Otros tipos de sistemas de ecuaciones

Hasta ahora hemos analizado los distintos tipos de sistemas de ecuaciones 2×2, es decir, con dos ecuaciones y dos incógnitas. Sin embargo, hay unos cuantos tipos de sistemas de ecuaciones menos conocidos. A continuación, vamos a ver cada uno de ellos.

Los sistemas de ecuaciones equivalentes son aquellos sistemas que tienen la misma solución, aunque no tengan la misma expresión matemática. Por ejemplo, los siguientes dos sistemas son equivalentes porque las ecuaciones de uno son múltiples de las ecuaciones del otro, lo que implica que tienen la misma solución.

$\left. \begin{array}{l} 5x+2y=-3 \\[2ex] x-3y=0 \end{array} \right\}\qquad \qquad \left. \begin{array}{l} 10x+4y=-6 \\[2ex] 2x-6y=0 \end{array} \right\}$

Por otro lado, los sistemas de ecuaciones también pueden ser no lineales, o dicho con otras palabras, puede que alguna de sus variables no sea de primer grado, como por ejemplo el siguiente sistema:

$\left. \begin{array}{l} x^2+3y=7 \\[2ex] \sqrt{5x+1}-9y^2=-4 \end{array} \right\}\$

Te dejo este enlace para que veas más ejemplos de sistemas de ecuaciones no lineales con raíces. Además, en esta página también se explica cómo se resuelven los sistemas de ecuaciones no lineales.

Además, los sistemas pueden estar compuestos por inecuaciones en lugar de ecuaciones. Fíjate en el siguiente ejemplo:

$\left. \begin{array}{l} 2x+5y<1 \\[2ex] 3x+8y\ge 6 \end{array} \right\}\$

Lógicamente, este tipo de sistemas se resuelven de manera distinta a un sistema de ecuaciones normal. Si estás más interesad@, puedes ver la resolución de sistemas de inecuaciones con dos incógnitas.

Finalmente, un sistema de ecuaciones puede estar formado por más de 2 ecuaciones y más de 2 incógnitas. Incluso el número de ecuaciones no tiene por qué ser igual al número de ecuaciones.

$\left. \begin{array}{l} 2x+y+4z=1 \\[2ex] 6x-2y-3z=6 \\[2ex] x-3y+4z=-1 \end{array} \right\}\$

Para solucionar estos tipos de sistemas se deben aplicar métodos más complejos, como por ejemplo el método de Gauss, el teorema de Rouché o la regla de Cramer (por determinantes). Si estás más interesad@ en este tema, te recomendamos que visites la web 👉👉www.matricesydeterminantes.com,👈👈 donde se explican paso a paso todos estos métodos.

Y aquí termina este post donde explicamos todos los tipos de sistemas de ecuaciones que existen. Esperamos que te hay gustado. Recuerda que puedes escribirnos en los comentarios qué te ha parecido, si te ha sido útil, qué mejorarías de la explicación, cualquier duda que te haya surgido, etc.

Tipos de sistemas de ecuaciones según su número de soluciones