En este post te explicamos cómo se resuelven los sistemas de inecuaciones con dos incógnitas mediante un ejemplo resuelto paso a paso. Además, encontrarás varios ejercicios resueltos de sistemas de inecuaciones con dos incógnitas para que puedas practicar.
Índice
Cómo resolver sistemas de inecuaciones con dos incógnitas
Para resolver un sistema de inecuaciones con dos incógnitas se deben hacer los siguientes pasos:
- Representar la región solución de la primera inecuación en una gráfica. Para ello se debe hacer:
- Transformar la desigualdad en una igualdad.
- Construir una tabla de valores, representar los puntos obtenidos en una gráfica, y trazar la recta que pasa por encima de los puntos. Entonces, la gráfica quedará dividida en dos regiones.
- Sustituir un punto de la gráfica en la inecuación para determinar qué región cumple con la desigualdad, dicha región es la solución de esa inecuación.
- Repetir el paso anterior para todas las inecuaciones que forman el sistema.
- La solución del sistema de inecuaciones con dos incógnitas es la intersección de las soluciones de todas las inecuaciones, es decir, la región donde se cumplen todas las inecuaciones del sistema.
Este procedimiento puede parecerte complicado, por eso, para que veas cómo se hacen los sistemas de inecuaciones con dos incógnitas, en el siguiente apartado hemos resuelto por pasos un sistema de inecuaciones de este tipo a modo de ejemplo.
Ejemplo de sistema de inecuaciones con dos incógnitas
A continuación, vamos a explicar paso a paso la resolución de un sistema de inecuaciones con dos incógnitas para que veas un ejemplo:
Paso 1: Representar la primera inecuación en una gráfica
Lo primero que debemos hacer es representar la primera inecuación en un gráfico. Para ello, transformamos la desigualdad en una igualdad:
Despejamos la incógnita y de la ecuación:
Entonces, tenemos que crear una tabla de valores otorgando valores a la incógnita x. Obteniendo 2 puntos es suficiente:
Ahora representamos en un gráfico los puntos obtenidos de la tabla de valores. Luego, trazamos la recta que pasa por encima de los puntos:
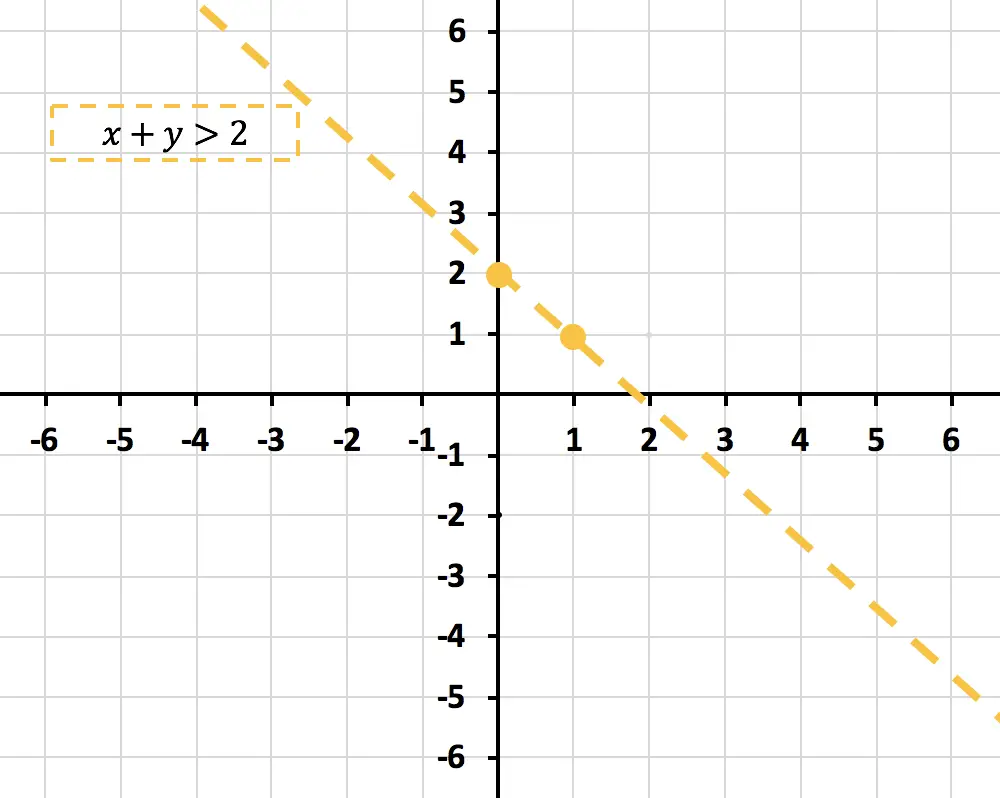
Fíjate que hemos representado la recta a trazos (- – – -) porque el signo de la inecuación no tiene el signo igual (>). Si el signo de la inecuación hubiera sido ≤ o ≥ tendríamos que haberla representado como una recta continua (——). Más abajo veremos por qué se debe hacer así.
Si te fijas, la recta divide la gráfica en dos lados. Pues debemos averiguar qué lado de la recta cumple la inecuación. Para ello, cogemos cualquier punto que no esté encima de la recta y comprobamos si cumple la inecuación.
Por ejemplo el punto (0,0):
❌
El punto (0,0) no cumple la inecuación, por lo tanto, la región que sí que cumplirá la inecuación será la otra, donde no está el (0,0). Esto es, el semiplano encima de la recta:
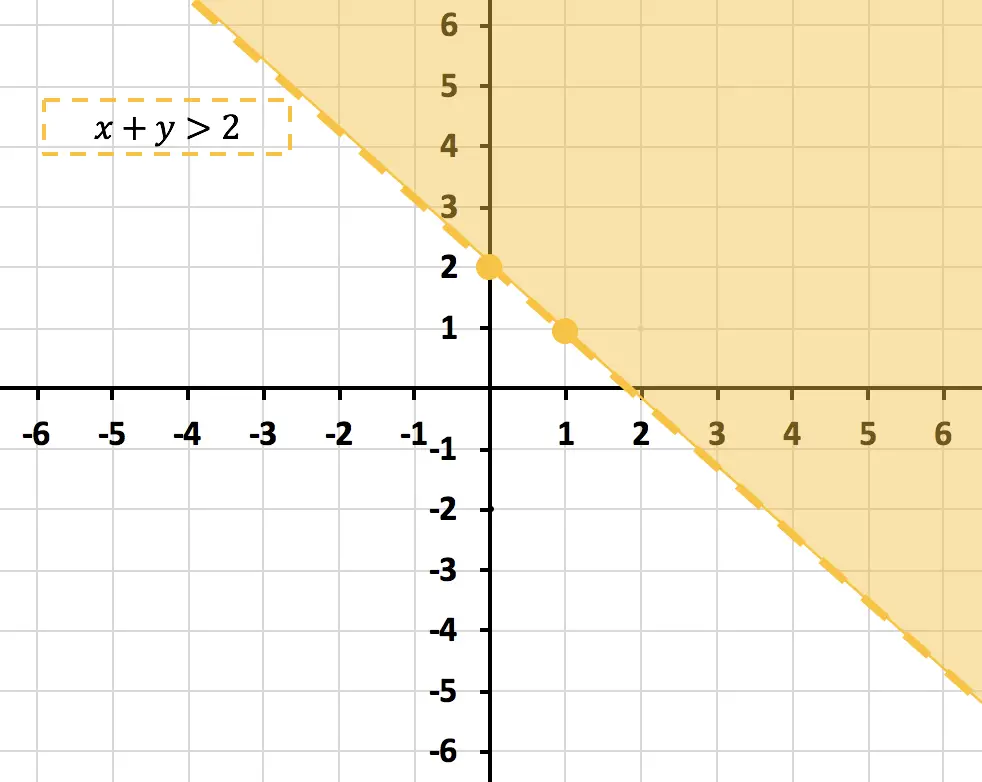
De manera que toda la zona pintada de amarillo cumple la inecuación Sin embargo, los puntos de encima la recta no cumplen la inecuación porque el signo > no tiene el igual. Por eso la hemos representado a trazos.
Si el signo de la inecuación es < o > los puntos encima de la recta no cumplen la inecuación (no son solución). Y, por tanto, representamos la recta a trazos: – – – –
En cambio, si el signo de la inecuación es ≤ o ≥ los puntos encima de la recta también cumplen la inecuación (son solución). Y, por tanto, representamos la recta de manera continua: ——
Paso 2: Representar en el mismo gráfico la otra inecuación del sistema
Ahora tenemos que repetir el mismo el proceso anterior con la otra inecuación. Así que representaremos en el mismo gráfico la inecuación Para ello, cambiamos el signo de la desigualdad por un igual:
Ahora despejamos la incógnita y, y creamos una tabla de valores:
Así pues, representamos en el mismo gráfico los puntos calculados en la tabla de valores, y luego unimos los puntos trazando una recta:
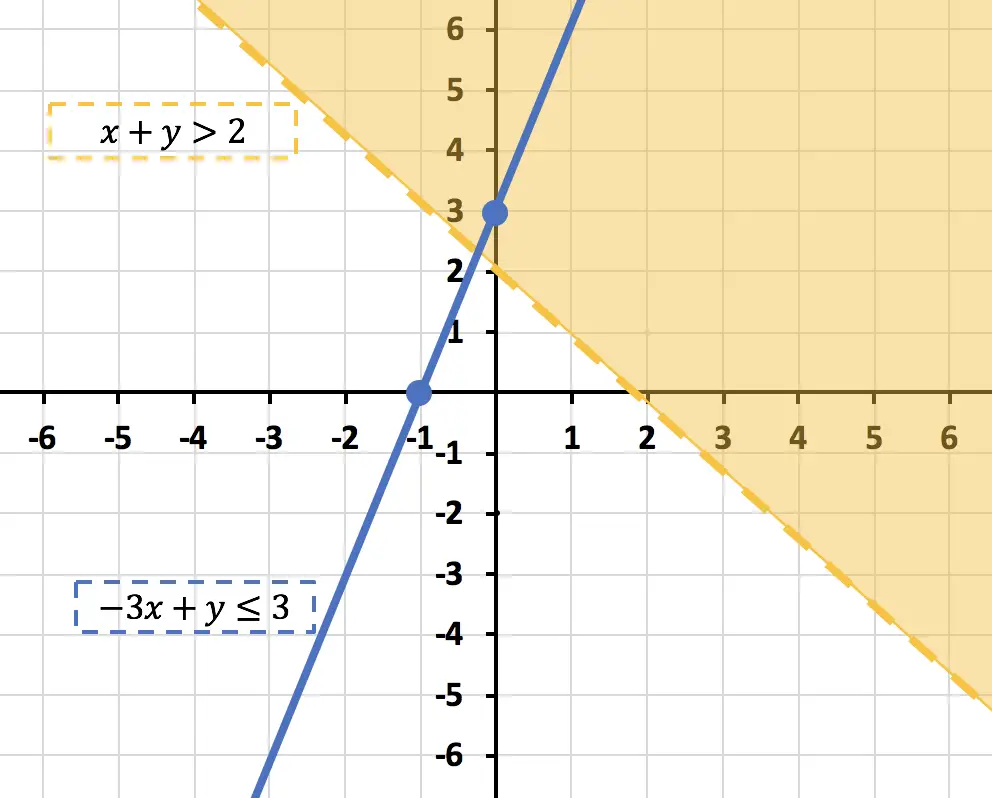
Fíjate que esta vez hemos representado la recta azul de manera continua, ya que el signo de la desigualdad tiene el signo igual (≤).
Igual que antes, ahora tenemos que comprobar qué lado de la recta azul cumple la inecuación. Para ello cogemos cualquier punto que no esté encima de la recta y comprobamos si cumple la inecuación:
✅
El punto (0,0) cumple con la desigualdad, por tanto, el lado que sí que cumplirá la inecuación será donde esté el (0,0). Es decir el semiplano a la derecha de la recta:
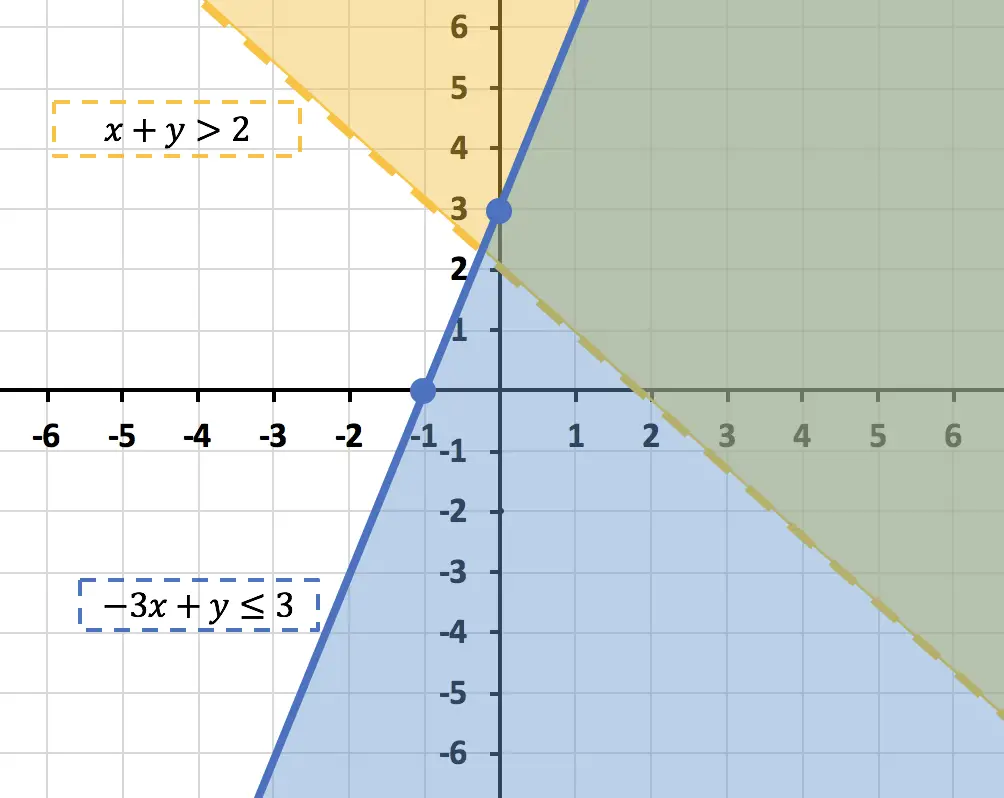
Toda la zona pintada de azul cumple la inecuación Incluso los puntos encima de la recta azul también cumplen con la inecuación, ya que tiene el signo ≤. Por eso la hemos representado de manera continua.
Paso 3: La solución del sistema es la zona donde se cumplen las dos inecuaciones
Una vez tenemos todas las inecuaciones del sistema representadas en un mismo gráfico, podemos determinar fácilmente la solución del sistema de inecuaciones con dos incógnitas.
La solución del sistema de inecuaciones es la región donde se cumplen ambas inecuaciones, es decir, la zona pintada por los dos colores:
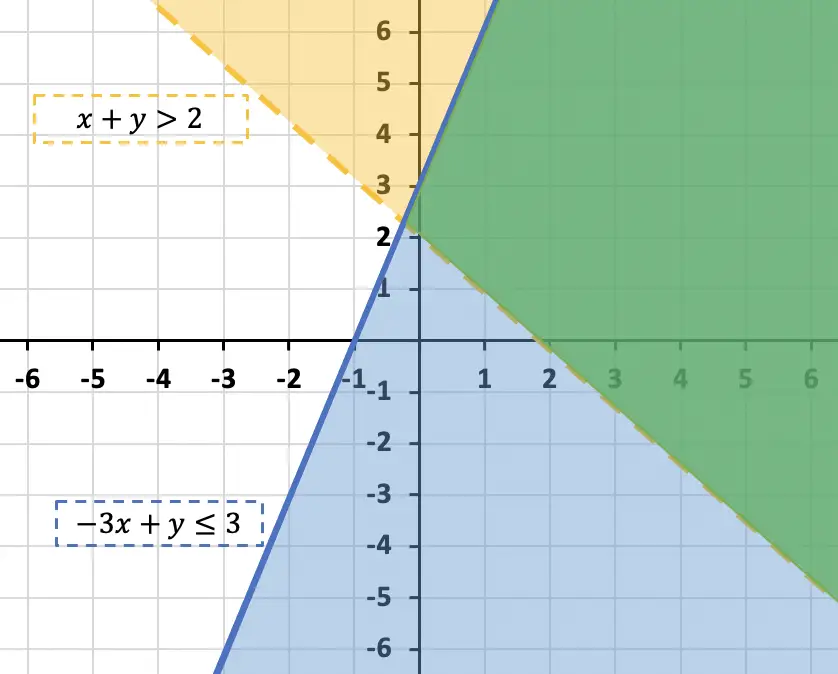
En conclusión, la región pintada de verde es la solución del sistema de inecuaciones con dos variables, o dicho de otra forma, los puntos de esa parte del gráfico verifican las dos inecuaciones del sistema.
Además, la parte de la recta azul dentro de la zona amarilla también es solución, ya que cumple las dos inecuaciones: cumple porque la inecuación también contiene el signo igual (≤), y cumple
porque está dentro de la zona pintada de amarillo.
Por otro lado, la parte de la recta discontinua amarilla que está dentro de la región azul no forma parte de la solución del sistema, ya que no cumple con la inecuación Esto es debido a que el signo de la desigualdad (>) no tiene el signo igual, lo que significa que no incluye los puntos de la propia recta.
Ejercicios resueltos de sistemas de inecuaciones con dos incógnitas
Una vez hemos visto cómo se calculan los sistemas de inecuaciones con dos incógnitas, te dejamos con varios ejercicios resueltos de este tipo de sistemas de inecuaciones. Están ordenados por dificultad pero, en general, encontrarás sistemas de inecuaciones con dos incógnitas tanto de nivel de ESO como de Bachillerato.
👇👇👇¡Si tienes alguna duda sobre la resolución de algún ejercicio o quieres que te resolvamos algún sistema de inecuaciones, puedes escribirla en los comentarios!👇👇👇
Ejercicio 1
Resuelve el siguiente sistema de dos inecuaciones con dos incógnitas:
Al representar gráficamente las dos inecuaciones del sistema, obtenemos el siguiente gráfico:
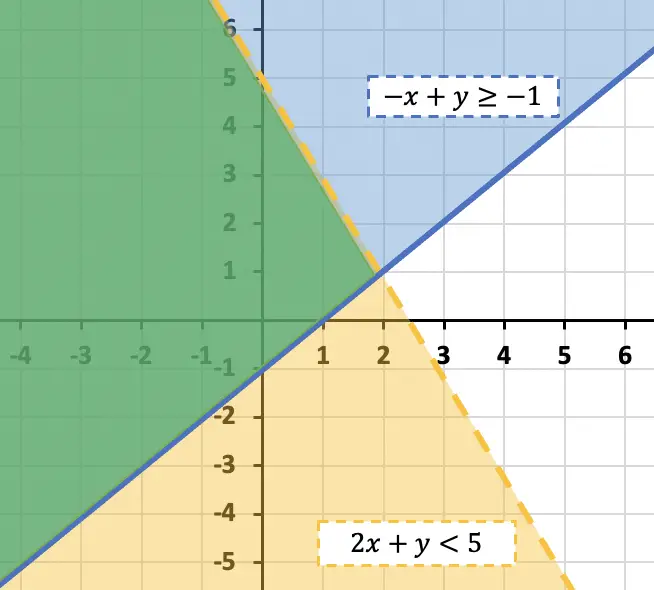
De manera que la solución del sistema de inecuaciones es la zona pintada de verde. Fíjate que en la solución se incluye la parte correspondiente de la recta azul porque la desigualdad tiene el signo igual (≥), por contra, la línea amarilla no forma parte de la solución porque la desigualdad no tiene el igual (<).
Ejercicio 2
Determina la región solución del siguiente sistema de dos inecuaciones con dos variables:
Al hacer la representación gráfica de las dos inecuaciones que forman el sistema obtenemos el siguiente gráfico:
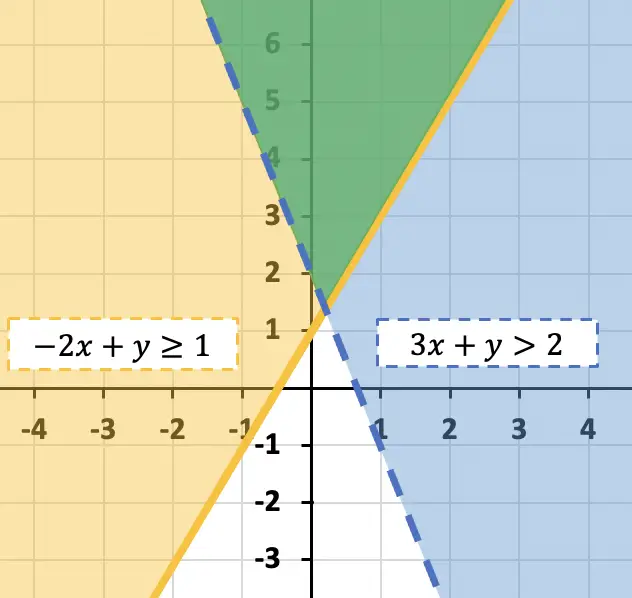
Por lo tanto, la solución del sistema de desigualdades con dos incógnitas corresponde a toda la zona pintada de color verde. En este problema la recta pintada de color azul (recta discontinua) no se incluye en la solución del sistema debido al signo >.
Ejercicio 3
Resuelve el siguiente sistema de tres inecuaciones con dos incógnitas:
Aunque el sistema tenga 3 inecuaciones en lugar de 2 inecuaciones, debemos aplicar el mismo procedimiento. Por lo tanto, al representar en un gráfico las tres inecuaciones obtenemos:
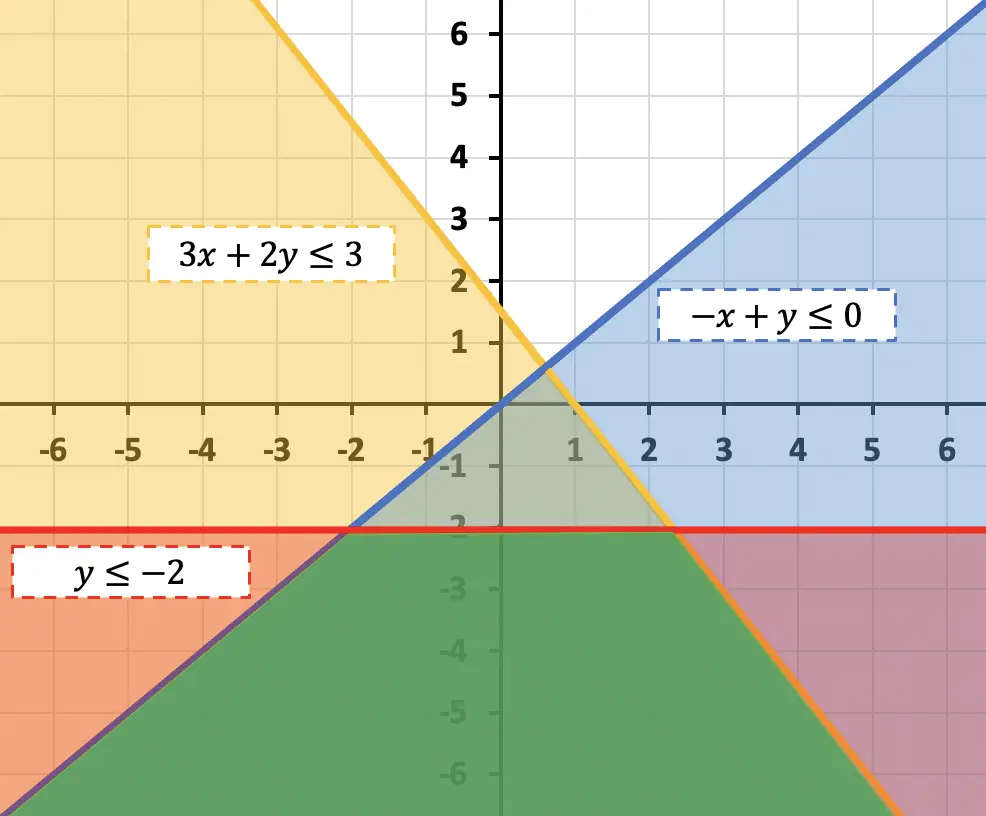
De modo que la solución del sistema de inecuaciones es toda la región representada de color verde.
Ejercicio 4
Soluciona el siguiente sistema de inecuaciones con dos incógnitas:
Para resolver el sistema de inecuaciones con dos incógnitas de este problema debemos representar la región solución de cada inecuación en un mismo gráfico:
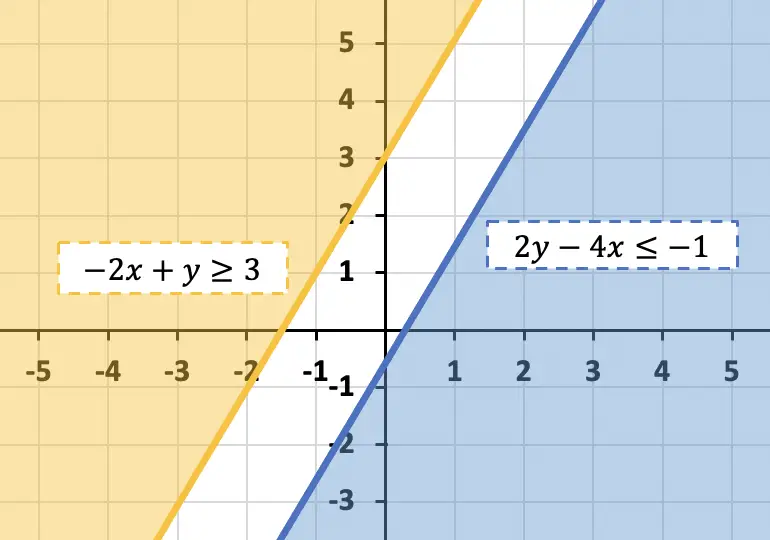
Sin embargo, en este caso las soluciones de las dos inecuaciones no tienen ninguna zona en común. En consecuencia, el sistema de inecuaciones con dos incógnitas no tiene solución.
Ejercicio 5
Encuentra la solución del siguiente sistema de 3 inecuaciones con 2 incógnitas:
Representamos gráficamente las tres inecuaciones del sistema:
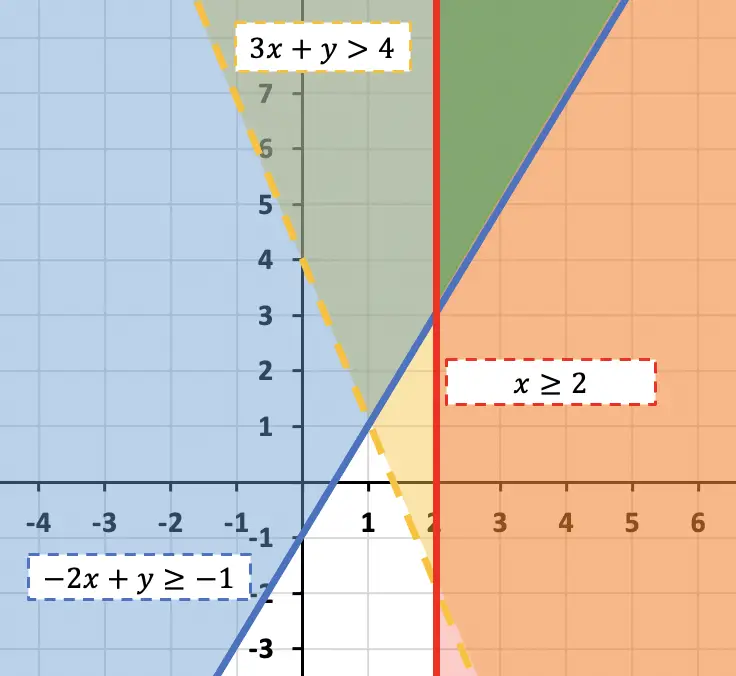
De forma que la solución del sistema de inecuaciones con dos incógnitas es toda la región donde coinciden las soluciones de las 3 inecuaciones, es decir, la zona representada de color verde.

