Inecuaciones de primer grado (o lineales)

En este post te explicamos qué es una inecuación de primer grado (o lineal) y cómo se resuelve. Encontrarás la explicación de cómo calcular este tipo de inecuaciones mediante un ejemplo resuelto por pasos y, finalmente, podrás practicar con ejercicios resueltos paso a paso de inecuaciones de primer grado.

¿Qué son las inecuaciones de primer grado?

Por ejemplo, la siguiente expresión algebraica es una inecuación de primer grado porque en lugar del signo igual tiene el signo de una desigualdad (>) y, además, la incógnita está elevada a la 1:

A continuación, vamos a ver cómo solucionar inecuaciones de primer grado, pero, lógicamente, antes debes saber qué significan los signos de las desigualdades. Por eso te dejamos el siguiente resumen de los signos de las inecuaciones.

Las inecuaciones de primer grado pueden tener 4 signos diferentes, cuyo significado son:

• El signo < significa «menor que». Por ejemplo 2<6.
• El signo ≤ quiere decir «menor o igual que». Por ejemplo 3≤3.
• El signo > indica «mayor que». Por ejemplo 8>5.
• El signo ≥ implica «mayor o igual que». Por ejemplo 6≥5.

 

Cómo resolver inecuaciones de primer grado

Para resolver una inecuación de primer grado se deben hacer los siguientes pasos:

1. Eliminar las fracciones de la inecuación multiplicando cada término por el mínimo común múltiplo de los denominadores.
2. Quitar los paréntesis de la inecuación aplicando la propiedad distributiva.
3. Trasponer los términos de manera que los monomios con x queden al primer miembro de la inecuación y los términos independientes al segundo miembro.
4. Agrupar los términos de cada miembro de la inecuación.
5. Despejar la incógnita x.
6. Expresar la solución de la inecuación de forma analítica, gráfica y por intervalos.

Para entender mejor cómo se resuelven las inecuaciones de primer grado o lineales, a continuación hemos resuelto paso a paso una inecuación de este tipo a modo de ejemplo.

Ejemplo de inecuación de primer grado resuelta

Vista la teoría sobre las inecuaciones de primer grado (o inecuaciones lineales), vamos a explicar paso a paso la resolución de una inecuación de primer grado utilizando el procedimiento que hemos visto en el apartado anterior:

Esta inecuación no tiene fracciones, pero sí que tiene paréntesis. Por lo tanto, aplicamos la propiedad distributiva para resolver el paréntesis:

En segundo lugar, transponemos los términos con x al lado izquierdo de la inecuación y los términos sin x al otro lado. Igual que con las ecuaciones, cuando un término cambia de lado también cambia de signo:

Sumamos y restamos los términos de cada miembro:

Y ahora despejamos la incógnita x. Ten en cuenta que como pasamos dividiendo un número negativo al otro lado, debemos girar el signo de la inecuación:

De manera que el conjunto solución de la inecuación de primer grado es:

Una vez hemos calculado el resultado numérico de la inecuación, debemos representarlo en la recta real. Para ello, primero representamos el -1 en la recta:

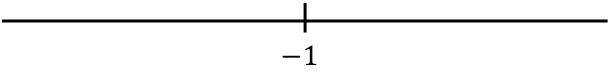
Ahora cogemos cualquier otro punto, por ejemplo x=0, y comprobamos si cumple la inecuación del ejercicio:

Efectivamente, 1 sí que es más pequeño 7, por lo que x=0 sí que cumple la inecuación. Entonces, como el 0 está a la derecha del -1, quiere decir que todos los números a la derecha del -1 también serán solución de la inecuación:

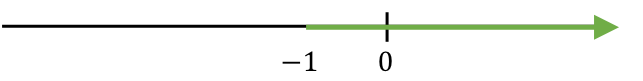
Ahora ya sabemos que todos los números a la derecha del -1 son solución. Pero…¿y el -1? ¿también forma parte de la solución?

En este caso el resultado de la inecuación es x>-1. Como el signo es “más pequeño que”, no está incluido el -1. En cambio, si el signo hubiera sido ≥, que quiere decir “más pequeño o igual que”, sí que se hubiera incluido el -1.

En consecuencia, como el -1 no se incluye se representa con un punto abierto, que consiste en un círculo vacío:

Finalmente, tenemos que representar el resultado de la inecuación en forma de intervalo. Para ello, hay que seguir las siguientes reglas:

A partir de estas reglas, en el intervalo debemos poner el inicio y el final de la solución. En nuestro caso, la solución va desde el -1 hasta el final de la recta, es decir +∞, de modo que el intervalo que le corresponde es:

Fíjate que hemos puesto en el lado del -1 un paréntesis porque el -1 está representado con un punto abierto. Asimismo, tanto +∞ como -∞ siempre van con paréntesis.

En la siguiente tabla puedes ver un resumen de cómo se expresa la solución de un inecuación de primer grado (o lineal) de manera numérica, gráfica y por intervalos:

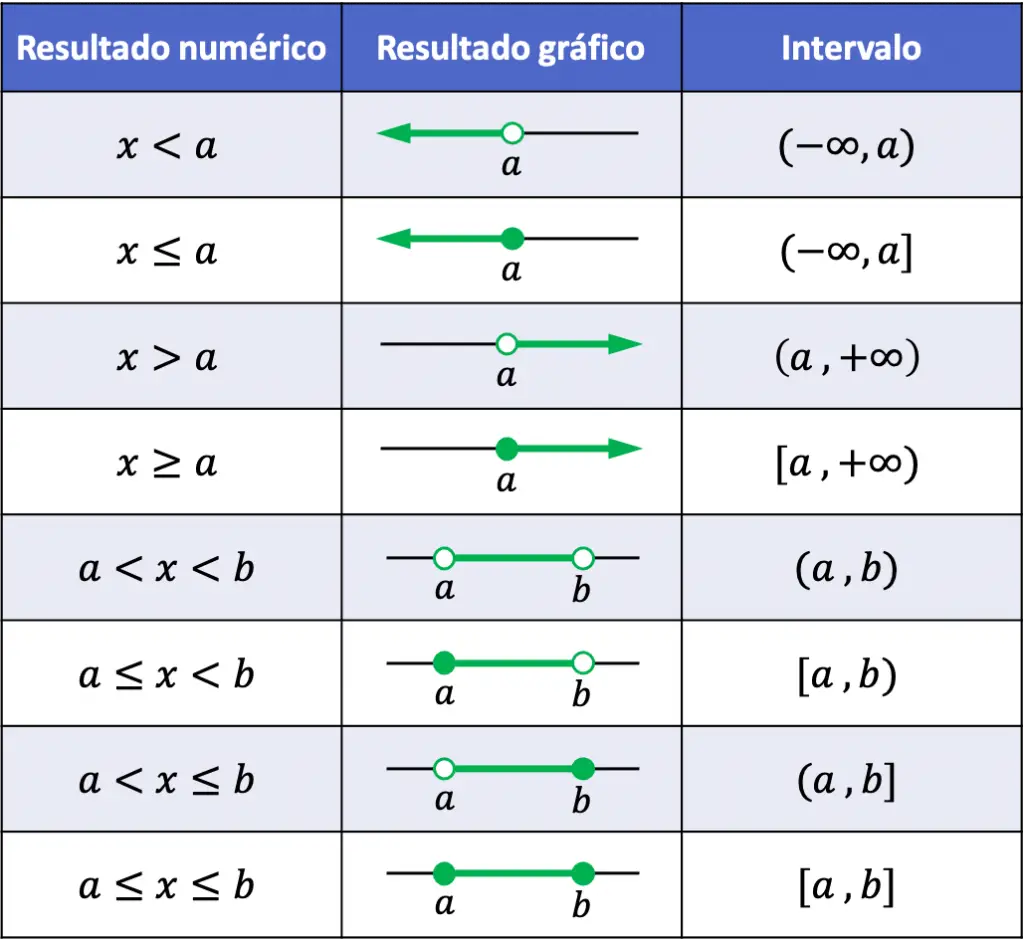
Como puedes comprobar, las inecuaciones de primer grado se calculan de manera muy similar a las ecuaciones lineales. Sin embargo, la solución de una inecuación no es solo un número como en las ecuaciones, sino es un rango de valores.

Ahora que ya sabes cómo calcular una inecuación de primer grado, el siguiente paso es aprender cómo resolver inecuaciones de segundo grado (o inecuaciones cuadráticas). De hecho, las inecuaciones de segundo grado se resuelven utilizando la base de las inecuaciones lineales, por tanto, ahora es un buen momento para ver cómo se hacen.

Ejercicios resueltos de inecuaciones de primer grado

Ejercicio 1

Calcula la siguiente inecuación de primer grado con paréntesis:

En primer lugar, operamos el paréntesis de la inecuación utilizando la propiedad distributiva:

Luego, ponemos los términos con x en un lado de la inecuación y los términos sin x en el otro lado:

Agrupamos los términos de cada lado:

Despejamos la incógnita de la inecuación:

Una vez hemos calculado la solución numérica de la inecuación, representamos dicha solución en la recta:

Y, por tanto, el intervalo solución de la inecuación es el siguiente:

 

Ejercicio 2

Resuelve la siguiente inecuación lineal con paréntesis:

Primero de todo, efectuamos los dos paréntesis que tiene la inecuación usando la propiedad distributiva:

Trasponemos los términos con x a un miembro de la inecuación y los términos sin x al otro miembro:

Agrupamos términos semejantes

Y despejamos la incógnita de la inecuación. En este caso cambiaremos de miembro un número negativo que está multiplicando, por lo tanto, tenemos que girar el signo de la inecuación:

Una vez hemos resuelto numéricamente la inecuación, representamos gráficamente su solución:

Y, por tanto, el intervalo solución de la inecuación es el siguiente:

 

Ejercicio 3

Resuelve la siguiente inecuación de primer grado con paréntesis y corchetes:

En primer lugar, aplicamos la propiedad distributiva 2 veces para eliminar los paréntesis y los corchetes de la inecuación:

Hacemos la transposición de términos:

Sumamos y restamos los términos de ambos lados de la inecuación:

Aislamos la incógnita x de la inecuación

De manera que la representación gráfica de la solución de la ecuación lineal es:

Entonces, el intervalo solución de la inecuación lineal es:

 

Ejercicio 4

Calcula la siguiente inecuación lineal con fracciones:

Lo primero que debemos hacer para calcular una desigualdad con fracciones es averiguar el mínimo común múltiplo de los denominadores (3, 6 y 9), que en este problema es 18:

En segundo lugar, multiplicamos cada término de la inecuación por el mínimo común múltiplo:

Luego simplificamos las fracciones de la inecuación dividendo el 18 entre cada denominador:

Calculamos las multiplicaciones:

Ponemos los monomios con incógnita en el primer miembro de la inecuación y los términos sin incógnita en el segundo miembro:

Sumamos y restamos los términos de cada miembro:

Y, finalmente, despejamos la incógnita x:

Así que la inecuación se cumple siempre que la x sea más pequeña o igual que 6. Por lo tanto, la representación de la inecuación en la recta numérica es:

Y el intervalo solución de la inecuación de primer grado con denominadores es:

 

Ejercicio 5

Resuelve la siguiente inecuación de primer grado con fracciones y paréntesis:

El primer paso para calcular una inecuación lineal con fracciones es determinar el mínimo común múltiplo entre sus denominadores:

Ahora multiplicamos cada elemento de la desigualdad por el mínimo común múltiplo hallado:

En tercer lugar, simplificamos las fracciones de la inecuación dividendo el 60 entre cada denominador:

Resolvemos los paréntesis y los corchetes de la inecuación aplicando la propiedad distributiva:

Movemos los elementos con x al lado izquierdo de la desigualdad y los términos sin x al lado derecho:

Sumamos y restamos los términos semejantes:

Y, por último, despejamos la incógnita x:

Recuerda que cuando en una inecuación cambiamos de lado un número negativo hay que invertir el signo de la desigualdad.

De modo que la inecuación se cumple cuando la variable x es más pequeña o igual que -2. Por lo que la representación en la recta de la inecuación es:

Y, en conclusión, el intervalo solución de la inecuación lineal con fracciones es:

 

También te puede interesar:

• Inecuaciones racionales
• Sistemas de inecuaciones con dos incógnitas (método gráfico)