Cómo resolver ecuaciones factorizadas (ejercicios resueltos)

En este post explicamos qué son las ecuaciones factorizadas y cómo se resuelven. Además, podrás practicar con ejercicios resueltos paso a paso de ecuaciones factorizadas.

Índice

¿Qué son las ecuaciones factorizadas?

Las ecuaciones factorizadas son ecuaciones formadas por productos de factores, es decir, las ecuaciones factorizadas son ecuaciones que solamente tienen paréntesis multiplicándose.

Por ejemplo, la siguiente ecuación está factorizada:

$(x-3)\cdot (x+5) \cdot (x^2-64)=0$

Aunque algunos matemáticos no hacen diferencia alguna, cabe destacar que los conceptos de ecuaciones factorizadas y ecuaciones factorizables significan cosas diferentes. Las ecuaciones factorizadas son aquellas que se han convertido en un producto de varios factores, en cambio, las ecuaciones factorizables son aquellas que se pueden factorizar en un producto de factores (pero que aún no se ha hecho) mediante procesos como la regla de Ruffini o extraer factor común.

Cómo resolver las ecuaciones factorizadas

Para resolver ecuaciones factorizadas simplemente se debe igualar cada uno de los factores a cero y resolver cada una de las ecuaciones resultantes. Las soluciones de cada ecuación resultante corresponden a las soluciones de la ecuación factorizada.

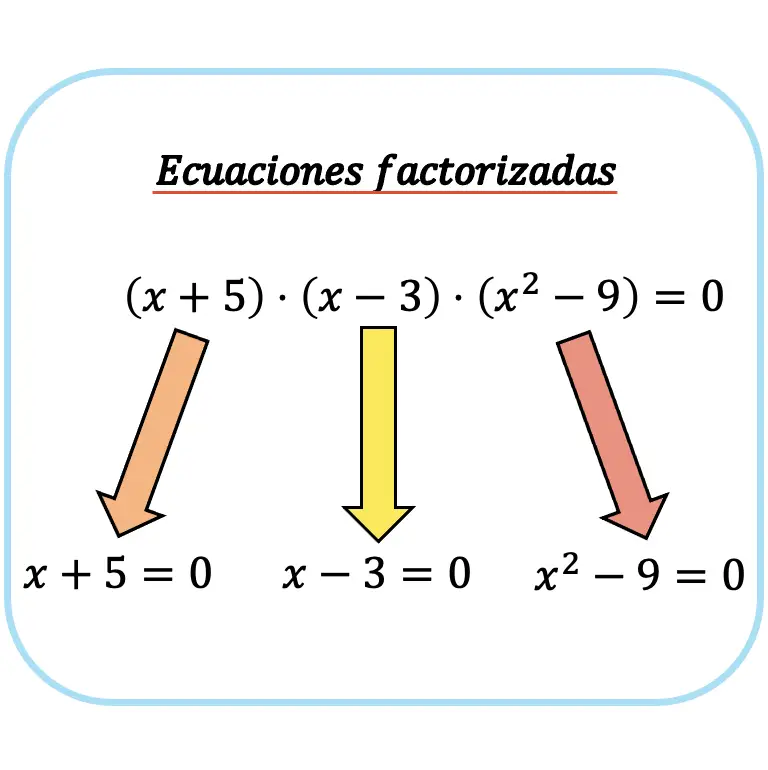
ecuaciones factorizadas y polinomicas eso

Este tipo de ecuaciones se resuelven así porque para que el producto de varios factores dé como resultado cero alguno de ellos debe ser igual a 0. Por lo tanto, la ecuación factorizada se cumplirá siempre que alguno de sus factores se anule.

Ejemplo de una ecuación factorizada resuelta

Una vez hemos visto la definición de ecuación factorizada, vamos a ver la resolución de un ejemplo explicando todos los pasos para que puedas ver exactamente cómo se hacen las ecuaciones factorizadas:

$(x-1)(2x+4) (x^2-25)=0$

Como hemos visto en el apartado anterior, para resolver una ecuación factorizada tenemos que igualar cada uno de los paréntesis a 0:

$x-1 =0$

$2x+4 =0$

$x^2-25=0$

Y una vez hemos igualado cada factor a cero, resolvemos cada una de las ecuaciones resultantes:

En la primera ecuación resultante solamente debemos despejar la x:

$x=1$

La segunda ecuación también es de primer grado, por tanto:

$2x=-4$

$x=\cfrac{-4}{2}$

$x=-2$

La tercera ecuación se trata de una ecuación de segundo grado incompleta, por tanto:

$x^2=25$

$x=\sqrt{25}$

$x=\pm 5$

En conclusión, la ecuación factorizada tiene 4 soluciones, que son:

$\bm{x=1 \qquad x=-2 \qquad x=5 \qquad x=-5}$

Las ecuaciones factorizadas son poco usuales, pero hay que saber resolverlas. Otro tipo de ecuaciones peculiares son las ecuaciones con valor absoluto, y aunque también aparecen poco debes saber cómo se resuelven (mucho más difíciles).

Ejercicios resueltos de ecuaciones factorizadas

Ejercicio 1

Resuelve la siguiente ecuación factorizada:

$(x+2)(x-6)(3x+12)=0$

Ver solución

Para resolver una ecuación factorizada primero debemos igualar cada uno de los factores a 0:

$x+2 =0$

$x-6 =0$

$3x+12=0$

Y luego solucionamos cada una de las ecuaciones resultantes. En este problema las tres ecuaciones son lineales, de modo que simplemente debemos despejar la incógnita x en cada una:

$x=-2$

$x=6$

$3x=-12$

$x=\cfrac{-12}{3}$

$x=-4$

En definitiva, las tres soluciones de la ecuación factorizada son:

$\bm{x=-2 \qquad x=6 \qquad x=-4}$

Ejercicio 2

Soluciona la siguiente ecuación factorizada:

$x(x^2-9)(5x-15)=0$

Ver solución

Para solucionar una ecuación factorizada debemos igualar el interior de cada paréntesis a cero:

$x=0$

$x^2-9 =0$

$5x-15=0$

Y luego solucionamos cada una de las ecuaciones que hemos obtenido:

$x=0$

$x^2=9$

$x=\sqrt{9}$

$x=\pm 3$

$5x=-15$

$x=\cfrac{-15}{5}$

$x=-3$

En definitiva, las cuatro soluciones de la ecuación factorizada son:

$\bm{x=0 \qquad x=3 \qquad x=-3 \qquad x=-3}$

Fíjate que en este caso la ecuación tiene una solución doble en x=-3.

Ejercicio 3

Calcula la siguiente ecuación factorizada:

$x^2(2x^2+5x+2)=0$

Ver solución

Para resolver cualquier ecuación factorizada tenemos que igualar cada uno de sus factores a 0:

$x^2=0$

$2x^2+5x+2 =0$

Y luego calculamos cada una de las ecuaciones resultantes. En este problema hemos obtenido dos ecuaciones de segundo grado: una incompleta y otra completa. Para determinar la ecuación cuadrática incompleta basta con hacer la raíz cuadrada, por contra, para resolver la ecuación cuadrática completa debemos aplicar la fórmula general:

$x^2=0$

$x=\sqrt{0}$

$\displaystyle x=\pm 0$

$2x^2+5x+2 =0$

$\displaystyle \begin{aligned} x & =\cfrac{-b\pm\sqrt{b^2-4ac}}{2a} \\[2ex] &= \cfrac{-5\pm\sqrt{5^2-4\cdot 2\cdot 2}}{2\cdot 2}\\[2ex] &=\cfrac{-5\pm\sqrt{9}}{4}\\[2ex] &=\cfrac{-5\pm 3}{4}\\[2ex] &=\begin{cases}\cfrac{-5+ 3}{4} = \cfrac{-2}{4} = \cfrac{-1}{2} \\[4ex]\cfrac{-5- 3}{4} = \cfrac{-8}{4} = -2 \end{cases} \end{aligned}$

En definitiva, las cuatro soluciones de la ecuación factorizada son:

$\bm{x=0 \qquad x=0 \qquad x=-2 \qquad x=} \mathbf{\cfrac{-1}{2}}$

Fíjate que la ecuación factorizada de este ejercicio tiene una solución doble en x=0.

Ejercicio 4

Resuelve la siguiente ecuación de tercer grado:

$x^3+8x^2-9x=0$

Pista: debes transformar la ecuación en una ecuación factorizada.

Ver solución

En este problema, tenemos una ecuación aún sin factorizar. Pero si nos fijamos bien, podemos factorizar la ecuación fácilmente sacando el factor común x:

$x(x^2+8x-9)=0$

Y una vez hemos factorizado la ecuación, solo nos queda aplicar el procedimiento de las ecuaciones factorizadas. Así que igualamos cada uno de sus factores a 0:

$x=0$

$x^2+8x-9 =0$

Y resolvemos cada ecuación resultante por separado:

$x=0$

$x^2+8x-9 =0$

$\displaystyle \begin{aligned} x & =\cfrac{-b\pm\sqrt{b^2-4ac}}{2a} \\[2ex] &= \cfrac{-8\pm\sqrt{8^2-4\cdot 1\cdot (-9)}}{2\cdot 1}\\[2ex] &=\cfrac{-8\pm\sqrt{100}}{2}\\[2ex] &=\cfrac{-8\pm 10}{2}\\[2ex] &=\begin{cases}\cfrac{-8+ 10}{2}= \cfrac{2}{2} =1 \\[4ex]\cfrac{-8-10}{2}= \cfrac{-18}{2} =-9\end{cases} \end{aligned}$