▷ Ecuaciones de cuarto grado

En este post te explicamos qué son las ecuaciones de cuarto grado (o ecuaciones cuárticas) y cómo se resuelven. Además, encontrarás varios ejercicios resueltos paso a paso de ecuaciones de cuarto grado para que puedas practicar.

Índice

Cómo resolver ecuaciones de cuarto grado

Para resolver una ecuación de cuarto grado, también llamada ecuación cuártica, se deben hacer los siguientes pasos:

Calcular dos raíces de la ecuación de cuarto grado con la regla de Ruffini.
Factorizar la ecuación de cuarto grado, es decir, transformar la ecuación cuártica en un producto de factores de las raíces calculadas en el paso anterior y una ecuación de segundo grado.
Resolver la ecuación de segundo grado hallada en el paso anterior aplicando la fórmula general.
Las soluciones de la ecuación de cuarto grado son las raíces obtenidas en el paso 1 más las soluciones de la ecuación de segundo grado.

Este método nos permitirá solucionar una ecuación de cuarto grado, sin embargo, para que lo entiendas mejor a continuación hemos resuelto un ejemplo por pasos.

Ejemplo de una ecuación de cuarto grado resuelta

Una vez hemos visto la teoría de las ecuaciones de cuarto grado, vamos a explicar la resolución de un ejemplo paso a paso para que puedas ver exactamente cómo se hacen este tipo de ecuaciones:

$x^4-x^3-7x^2+x+6=0$

En primer lugar, debemos determinar dos raíces de la ecuación polinómica de cuarto grado. Para ello, aplicamos la regla de Ruffini:

ecuaciones de cuarto grado con la regla de ruffini

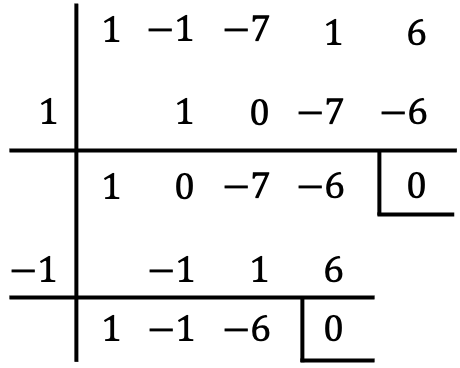
Recuerda que la raíz de una ecuación polinómica siempre es un divisor del término independiente. Por lo tanto, tenemos que ir aplicando la regla de Ruffini con divisores del término independiente hasta encontrar dos que den como resultado un resto nulo.

De la división con la regla de Ruffini hemos obtenido, por un lado, dos raíces de la ecuación (x=1, x=-1). Y, por otro lado, hemos obtenido un polinomio de segundo grado en el cociente de la división:

$1 \quad -1 \quad -6 \quad \color{orange}\bm{\longrightarrow}\color{black} \quad 1x^2 - 1x-6$

De manera que podemos factorizar la ecuación de cuarto grado con las raíces y el polinomio de segundo grado obtenidos:

$\begin{array}{c}x^4-x^3-7x^2+x+6=0\\[1.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] (x-1)(x+1)(x^2-x-6)=0\end{array}$

Entonces, ahora tenemos que igualar a cero el polinomio cuadrático obtenido y resolver la ecuación resultante:

$x^2-x-6=0$

De este modo hemos conseguido simplificar la ecuación de cuarto grado en una ecuación de segundo grado. Y este tipo de ecuaciones se pueden resolver fácilmente aplicando la fórmula general:

$\begin{aligned}x&=\cfrac{-(-1)\pm\sqrt{(-1)^2-4\cdot 1\cdot (-6)}}{2\cdot 1}=\\[2ex]&=\cfrac{1 \pm\sqrt{25}}{2}=\cfrac{1\pm 5}{2}= \begin{cases}\cfrac{1+5}{2}=\cfrac{6}{2}=3\\[4ex]\cfrac{1-5}{2}=\cfrac{-4}{2}=-2\end{cases}\end{aligned}$

En resumen, las cuatro soluciones de la ecuación de grado 4 son las dos soluciones calculadas de la ecuación de segundo grado más las dos soluciones obtenidas previamente de la regla de Ruffini:

$\bm{x=1\qquad x=-1\qquad x=3\qquad x=-2}$

De esta forma hemos podido resolver la ecuación de cuarto grado simplemente aplicando la regla de Ruffini y la fórmula general de las ecuaciones de segundo grado.

Ecuaciones bicuadradas

Un tipo de ecuaciones de cuarto grado son las ecuaciones bicuadradas, que tienen la siguiente peculiaridad:

Las ecuaciones bicuadradas son ecuaciones de cuarto grado que solamente tienen términos de grado par, es decir, la expresión algebraica de una ecuación bicuadrada es:

$ax^4+bx^2+c=0$

Sin embargo, para resolver las ecuaciones bicuadradas se debe aplicar un procedimiento más complicado, en concreto, se debe hacer un cambio de variable. Puedes ver cómo resolver ecuaciones bicuadradas haciendo click en este enlace.

Ejercicios resueltos de ecuaciones de cuarto grado

Ejercicio 1

Resuelve la siguiente ecuación de cuarto grado:

$x^4+5x^3-20x-16=0$

Ver solución

Primero de todo, calculamos dos raíces de la ecuación de cuarto grado incompleta aplicando el método de Ruffini:

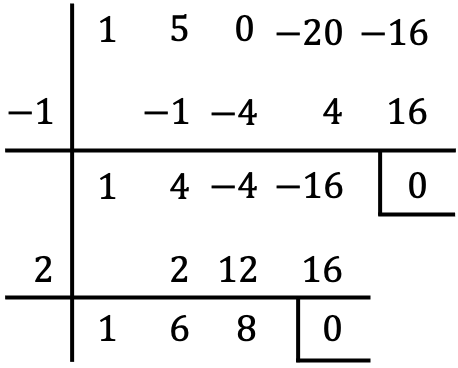
Factorizamos la ecuación de cuarto grado con las raíces y el polinomio cuadrático hallados de la división por Ruffini:

$\begin{array}{c}x^4+5x^3-20x-16=0\\[1.5ex]\bm{\downarrow}\\[1.5ex] (x+1)(x-2)(x^2+6x+8)=0\end{array}$

Ahora igualamos a cero el polinomio cuadrático obtenido:

$x^2+6x+8=0$

Y resolvemos la ecuación cuadrática obtenida utilizando la fórmula general:

$\begin{aligned}x&=\cfrac{-6\pm\sqrt{6^2-4\cdot 1\cdot 8}}{2\cdot 1}=\\[2ex]&=\cfrac{-6 \pm\sqrt{4}}{2}=\cfrac{-6\pm 2}{2}= \begin{cases}\cfrac{-6+2}{2}=\cfrac{-4}{2}=-2\\[4ex]\cfrac{-6-2}{2}=\cfrac{-8}{2}=-4\end{cases}\end{aligned}$

Por lo tanto, las 4 soluciones de la ecuación de cuarto grado son:

$\bm{x=-1\qquad x=2\qquad x=-2\qquad x=-4}$

Ejercicio 2

Soluciona la siguiente ecuación cuártica:

$x^4-2x^3-19x^2+8x+60=0$

Ver solución

Lo primero que debemos hacer para calcular la ecuación de cuarto grado es determinar dos raíces aplicando la regla de Ruffini:

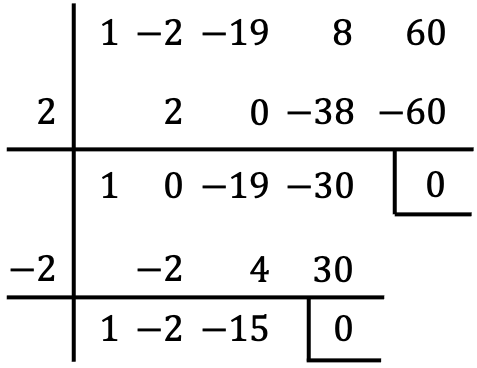
En segundo lugar, hacemos la factorización de la ecuación de cuarto grado con las raíces halladas y el polinomio de segundo grado obtenido de la regla de Ruffini:

$\begin{array}{c}x^4-2x^3-19x^2+8x+60=0\\[1.5ex]\bm{\downarrow}\\[1.5ex] (x-2)(x+2)(x^2-2x-15)=0\end{array}$

Luego igualamos a cero el polinomio de segundo grado obtenido:

$x^2-2x-15=0$

Y calculamos las dos soluciones de la ecuación de segundo grado:

$\begin{aligned}x&=\cfrac{-(-2)\pm\sqrt{(-2)^2-4\cdot 1\cdot (-15)}}{2\cdot 1}=\\[2ex]&=\cfrac{2\pm\sqrt{64}}{2}=\cfrac{2\pm 8}{2}= \begin{cases}\cfrac{2+8}{2}=\cfrac{10}{2}=5\\[4ex]\cfrac{2-8}{2}=\cfrac{-6}{2}=-3\end{cases}\end{aligned}$

En conclusión, las cuatro soluciones de la ecuación de cuártica son:

$\bm{x=2\qquad x=-2\qquad x=5\qquad x=-3}$

Ejercicio 3

Calcula la siguiente ecuación de cuarto grado:

$x^4+x^3-30x^2-72x=0$

Ver solución

En este problema podemos simplificar la ecuación de cuarto grado sacando el factor común x:

$x(x^3+x^2-30x-72)=0$

De esta forma hemos podido determinar una raíz de la ecuación de cuarto grado (x=0) sin aplicar la regla de Ruffini, y simplemente tenemos que calcular una raíz de la ecuación de tercer grado obtenida:

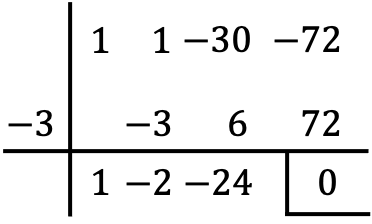
Entonces, transformamos la ecuación de cuarto grado en un producto de factores:

$\begin{array}{c}x^4+x^3-30x^2-72x=0\\[1.5ex]\bm{\downarrow}\\[1.5ex] x(x+3)(x^2-2x-24)=0\end{array}$

Luego igualamos a cero el polinomio de segundo grado obtenido de la división por Ruffini:

$x^2-2x-24=0$

Y, por último, hallamos las dos soluciones de la ecuación de segundo grado:

$\begin{aligned}x&=\cfrac{-(-2)\pm\sqrt{(-2)^2-4\cdot 1\cdot (-24)}}{2\cdot 1}=\\[2ex]&=\cfrac{2\pm\sqrt{100}}{2}=\cfrac{2\pm 10}{2}= \begin{cases}\cfrac{2+10}{2}=\cfrac{12}{2}=6\\[4ex]\cfrac{2-10}{2}=\cfrac{-8}{2}=-4\end{cases}\end{aligned}$

En definitiva, las cuatro raíces de la ecuación de cuarto grado son son:

$\bm{x=0\qquad x=-3\qquad x=6\qquad x=-4}$

También te puede interesar:

Cómo resolver ecuaciones de cuarto grado

Ejemplo de una ecuación de cuarto grado resuelta

Ecuaciones bicuadradas

Ejercicios resueltos de ecuaciones de cuarto grado

Ejercicio 1

Ejercicio 2

Ejercicio 3

Deja un comentario Cancelar respuesta