En este post te explicamos cómo se resuelven las ecuaciones de tercer grado (o ecuaciones cúbicas). También encontrarás ejemplos de ecuaciones de tercer grado resueltas y, además, podrás practicar con ejercicios resueltos paso a paso de este tipo de ecuaciones.
Índice
¿Qué son las ecuaciones de tercer grado (o ecuaciones cúbicas)?
Las ecuaciones de tercer grado, también llamadas ecuaciones cúbicas, son ecuaciones que tienen la incógnita elevada al cubo. Las ecuaciones de tercer grado se resuelven con la regla de Ruffini.
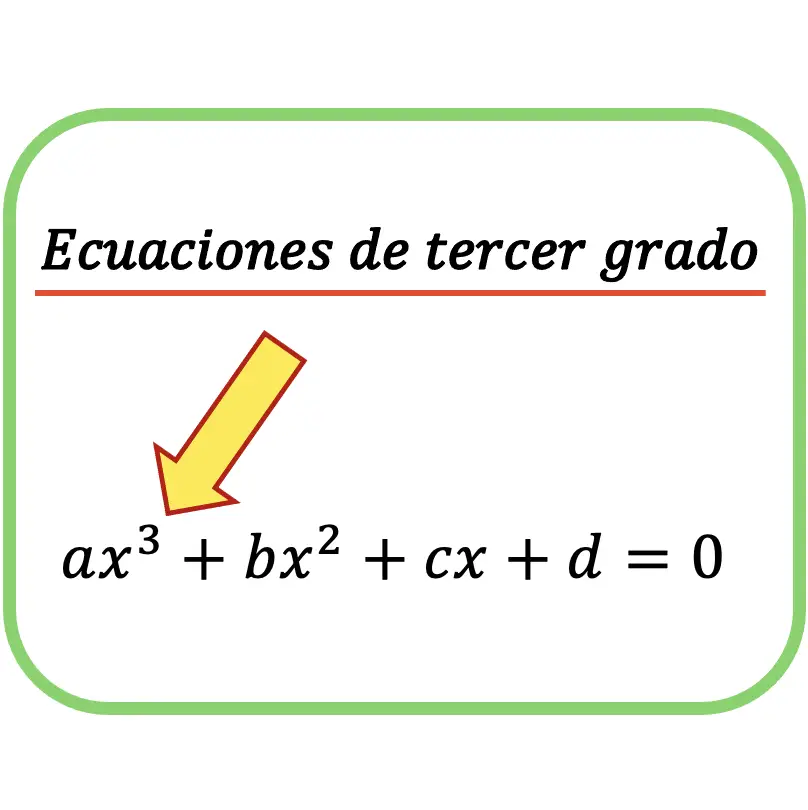
Además, para que una ecuación sea de tercer grado no es indispensable que tenga término cuadrático, término lineal y término independiente. Sino que una ecuación solamente necesita un término cúbico para que se considere de tercer grado, es indiferente si tiene o no los otros términos.
Cómo resolver ecuaciones de tercer grado
Los pasos que se deben hacer para resolver las ecuaciones de tercer grado (o ecuaciones cúbicas) son:
- Calcular una raíz de la ecuación de tercer grado con la regla de Ruffini.
- Factorizar la ecuación de tercer grado, es decir, transformar la ecuación cúbica en un producto de factores formado por la raíz calculada en el paso anterior y una ecuación de segundo grado.
- Resolver la ecuación de segundo grado hallada en el paso anterior.
- Las soluciones de la ecuación de tercer grado son la raíz obtenida en el paso 1 y las soluciones de la ecuación de segundo grado.
Este método nos permitirá hacer cualquier tipo de ecuación de tercer grado o cúbica, sin embargo, para que lo entiendas mejor a continuación hemos resuelto un ejemplo paso a paso.
Ejemplo de una ecuación de tercer grado resuelta
Una vez hemos visto la teoría de las ecuaciones de tercer grado (o cúbicas), vamos a explicar la resolución de un ejemplo paso a paso para que puedas ver exactamente cómo se hacen este tipo de ecuaciones:
Lo primero que debemos hacer es calcular una raíz de la ecuación con la regla de Ruffini.
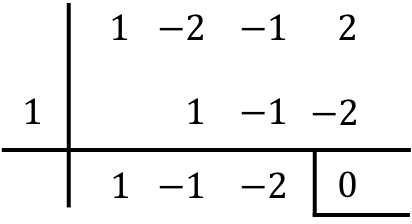
Recuerda que la raíz de una ecuación polinómica siempre es un divisor del término independiente. Por lo tanto, tenemos que ir aplicando la regla de Ruffini con divisores del término independiente hasta encontrar uno que dé como resultado un resto nulo.
De la división con la regla de Ruffini hemos obtenido, por un lado, una raíz de la ecuación (x=1). Y, por otro lado, hemos obtenido un polinomio de segundo grado en el cociente de la división:
De modo que podemos factorizar la ecuación de tercer grado con la raíz y el polinomio cuadrático calculados:
Por lo tanto, ahora simplemente debemos igualar a cero este polinomio obtenido y resolver la ecuación de segundo grado resultante:
Así que aplicamos la fórmula general de las ecuaciones de segundo grado para resolverla:
![\begin{aligned} x&= \cfrac{-b\pm \sqrt{b^2-4ac}}{2a} = \\[2ex] & =\cfrac{-(-1) \pm \sqrt{(-1)^2 -4 \cdot 1 \cdot (-2) }}{2 \cdot 1} = \\[2ex] & = \cfrac{+1 \pm \sqrt{1 +8 }}{2}= \\[2ex] &=\cfrac{1 \pm \sqrt{9}}{2}= \\[1.5ex] & =\cfrac{1 \pm 3}{2}= \begin{cases} \cfrac{1+3}{2} = \cfrac{4}{2} = \bm{2} \\[4ex] \cfrac{1-3}{2} = \cfrac{-2}{2} = \bm{-1} \end{cases} \end{aligned}](https://www.ejerciciosecuaciones.com/wp-content/ql-cache/quicklatex.com-642546025546176473c1a519c3a287d9_l3.svg "Rendered by QuickLaTeX.com")
En conclusión, las soluciones de la ecuación de tercer grado son las dos soluciones de la ecuación de segundo grado y la raíz calculada previamente:
Ejercicios resueltos de ecuaciones de tercer grado
A continuación, te dejamos con varios ejercicios resueltos paso a paso de ecuaciones de tercer grado (o ecuaciones cúbicas). Están ordenados por dificultad, de manera que las primeras ecuaciones son las más fáciles y las últimas ecuaciones las más difíciles. Si tienes alguna duda (o alguna sugerencia) sobre el método que hemos visto o sobre la resolución de algún ejercicio, no dudes en escribirla en los comentarios que te responderemos. 👇👇👇
Ejercicio 1
Resuelve la siguiente ecuación de tercer grado:
En primer lugar, aplicamos la regla de Ruffini para calcular una raíz de la ecuación cúbica:
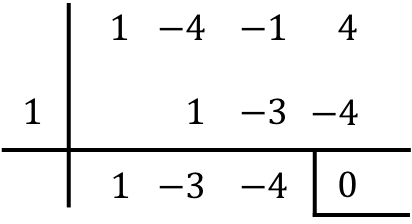
Ahora hacemos la factorización de la ecuación con el resultado de la regla de Ruffini:
Y, finalmente, solucionamos la ecuación de segundo grado utilizando la fórmula general:
![\begin{aligned} x & = \cfrac{ -b \pm \sqrt{b^2 - 4ac}}{2a} \\[2ex] &= \cfrac{-(-3) \pm \sqrt{(-3)^2 - 4 \cdot 1 \cdot (-4)}}{2\cdot 1}\\[2ex] &= \cfrac{+3 \pm \sqrt{9+16}}{2}\\[2ex] &= \cfrac{3 \pm \sqrt{25}}{2}\\[1.5ex] &= \cfrac{3 \pm 5}{2}= \begin{cases} \cfrac{3+5}{2} = \cfrac{8}{2} =\bm{4} \\[3ex] \cfrac{3-5}{2} = \cfrac{-2}{2} =\bm{-1} \end{cases}\end{aligned}](https://www.ejerciciosecuaciones.com/wp-content/ql-cache/quicklatex.com-45559616a2c721e69edd2f53ab76f479_l3.svg "Rendered by QuickLaTeX.com")
En definitiva, las tres soluciones de la ecuación cúbica son:
Ejercicio 2
Resuelve la siguiente ecuación cúbica:
Primero de todo aplicamos el método de Ruffini para hallar una raíz de la ecuación:
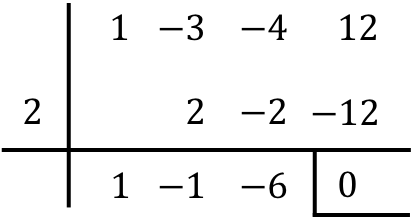
En segundo lugar, factorizamos la ecuación polinómica:
Y, por último, calculamos la ecuación cuadrática resultante aplicando la fórmula general:
![\begin{aligned} x & = \cfrac{ -b \pm \sqrt{b^2 - 4ac}}{2a} \\[2ex] & = \cfrac{-(-1) \pm \sqrt{(-1)^2 - 4 \cdot 1 \cdot (-6)}}{2\cdot 1}\\[2ex] & = \cfrac{+1 \pm \sqrt{1+24}}{2}= \\[2ex] & =\cfrac{1 \pm \sqrt{25}}{2}= \\[1.5ex] & =\cfrac{1 \pm 5}{2}= \begin{cases} \cfrac{1+5}{2} = \cfrac{6}{2} =\mathbf{3} \\[3ex] \cfrac{1-5}{2} = \cfrac{-4}{2} =\bm{-2} \end{cases}\end{aligned}](https://www.ejerciciosecuaciones.com/wp-content/ql-cache/quicklatex.com-b5fd7a6a20f9a7573f616c89b5706067_l3.svg "Rendered by QuickLaTeX.com")
De forma que las tres soluciones de la ecuación de tercer grado son:
Ejercicio 3
Calcula la siguiente ecuación de tercer grado:
El primer paso es hallar una raíz de la ecuación cúbica mediante la regla de Ruffini (o división sintética):
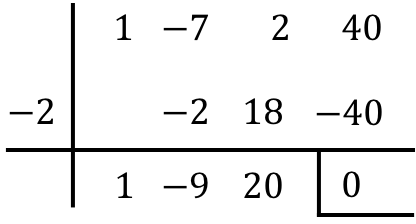
Luego transformamos la ecuación en un producto de factores a partir del resultado obtenido en el paso anterior:
En tercer lugar, calculamos la ecuación de segundo grado usando la fórmula general:
![\begin{aligned} x &= \cfrac{ -b \pm \sqrt{b^2 - 4ac}}{2a} \\[2ex] & = \cfrac{-(-9) \pm \sqrt{(-9)^2 - 4 \cdot 1 \cdot 20}}{2\cdot 1}\\[2ex] & = \cfrac{+9 \pm \sqrt{81-80}}{2}\\[2ex] & =\cfrac{9 \pm \sqrt{1}}{2}\\[1.5ex] & = \cfrac{9\pm 1}{2}= \begin{cases} \cfrac{9+1}{2} = \cfrac{10}{2} =\mathbf{5} \\[3ex] \cfrac{9-1}{2} = \cfrac{8}{2} =\mathbf{4} \end{cases} \end{aligned}](https://www.ejerciciosecuaciones.com/wp-content/ql-cache/quicklatex.com-013ef829f52cc85cd918f7ca8a304c5f_l3.svg "Rendered by QuickLaTeX.com")
En resumen, las 3 soluciones de la ecuación de tercer grado son:
Ejercicio 4
Soluciona la siguiente ecuación cúbica:
Primero hallamos una raíz de la ecuación cúbica mediante la regla de Ruffini:
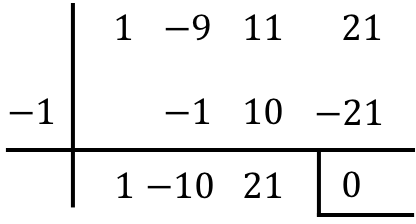
Entonces, podemos factorizar la ecuación de tercer grado:
Para terminar, resolvemos la ecuación de grado 2 aplicando su fórmula correspondiente:
![\begin{aligned} x & = \cfrac{ -b \pm \sqrt{b^2 - 4ac}}{2a} \\[2ex] & =\cfrac{-(-10) \pm \sqrt{(-10)^2 - 4 \cdot 1 \cdot 21}}{2\cdot 1}\\[2ex] & = \cfrac{+10 \pm \sqrt{100-84}}{2}\\[2ex] & = \cfrac{10 \pm \sqrt{16}}{2}\\[1.5ex] & =\cfrac{10\pm 4}{2}= \begin{cases} \cfrac{10+4}{2} = \cfrac{14}{2} =\bm{7} \\[3ex] \cfrac{10-4}{2} = \cfrac{6}{2} =\bm{3} \end{cases} \end{aligned}](https://www.ejerciciosecuaciones.com/wp-content/ql-cache/quicklatex.com-d4b2c724ac30f732a0924b98ffdda888_l3.svg "Rendered by QuickLaTeX.com")
De manera que las soluciones de la ecuación cúbica son la raíz calculada en el primer paso más las 2 soluciones de la ecuación cuadrática:
Ejercicio 5
Resuelve la siguiente ecuación de tercer grado sin término independiente:
La ecuación de este problema se trata de una ecuación de tercer grado incompleta, ya que no tiene término independiente. Por lo tanto, podemos resolver la ecuación de tercer grado sin aplicar la regla de Ruffini, simplemente tenemos que sacar factor común.
Así pues, primero extraemos el factor común x de la ecuación cúbica:
Y ahora aplicamos el mismo procedimiento que se utiliza para resolver las ecuaciones de segundo grado incompletas, esto es, igualamos cada factor a 0:
![\displaystyle x(x^2+9x+18)=0 \begin{cases}\bm{x= 0} \\[2ex] x^2+9x+18=0 \end{cases}](https://www.ejerciciosecuaciones.com/wp-content/ql-cache/quicklatex.com-fe03633b338544f53aeb7f819a03f2ef_l3.svg "Rendered by QuickLaTeX.com")
De modo que una solución de la ecuación de grado 3 será x=0. Y para hallar las otras dos soluciones tenemos que calcular la ecuación de segundo grado obtenida en el paso anterior:
![\begin{aligned} x & = \cfrac{ -b \pm \sqrt{b^2 - 4ac}}{2a} \\[2ex] & =\cfrac{-9 \pm \sqrt{9^2 - 4 \cdot 1 \cdot 18}}{2\cdot 1}\\[2ex] & = \cfrac{-9 \pm \sqrt{81-72}}{2}\\[2ex] & = \cfrac{-9 \pm \sqrt{9}}{2}\\[1.5ex] & =\cfrac{-9\pm 3}{2}= \begin{cases} \cfrac{-9+3}{2} = \cfrac{-6}{2} =\bm{-3} \\[3ex] \cfrac{-9-3}{2} = \cfrac{-12}{2} =\bm{-6}\end{cases} \end{aligned}](https://www.ejerciciosecuaciones.com/wp-content/ql-cache/quicklatex.com-8174e6a7b319d30f65f922c7c798e67f_l3.svg "Rendered by QuickLaTeX.com")
Por lo tanto, las tres soluciones de la ecuación de tercer grado incompleta son:
Soluciones de una ecuación de tercer grado
En los apartados anteriores hemos visto cómo se calculan numéricamente las soluciones de las ecuaciones de tercer grado. Sin embargo, en ocasiones puede que solo nos interese saber cómo son estas soluciones en lugar de conocer su valor exacto. Pues esto se puede hacer con una operación matemática llamada discriminante.
El discriminante de una ecuación de tercer grado se calcula con la siguiente fórmula:
![\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white,shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \Delta = b^2c^2-4ac^3-4b^3d-27a^2d^2+18abcd \end{empheq}](https://www.ejerciciosecuaciones.com/wp-content/ql-cache/quicklatex.com-b038ec96d117952f7ee0b8cf56b67bb1_l3.svg "Rendered by QuickLaTeX.com")
El valor del discriminate de una ecuación de tercer grado (o ecuación cúbica) determina el tipo de soluciones de dicha ecuación:
- Si el discriminante es positivo (Δ>0), la ecuación de tercer grado tiene tres soluciones reales diferentes.
- Si el discriminante es igual a cero (Δ=0), la ecuación de tercer grado tiene soluciones múltiples y todas ellas son reales. Por lo tanto, la ecuación puede tener una solución triple o una solución doble junto a una solución simple.
- Si el discriminante es negativo (Δ<0), la ecuación de tercer grado tiene una solución real y dos soluciones complejas conjugadas.
Quiero hacer una ecuación y necesito ayuda
Hola Kenel,
Puedes plantear aquí la ecuación e intentaré ayudarte. 🙂
Ejemplos de ecuaciones cuadráticas con una variable
Hola Junior,
Puedes encontrar varios ejemplos de este tipo de ecuaciones resueltas en el artículo correspondiente de nuestra página web. Para encontrarlo, puedes utilizar el buscador que hay en la barra lateral (o abajo del todo si estás visitando la web desde un móvil).
Buenos días. Muchas gracias me ha sido de mucha utilidad
Dado que ya no me acordaba de ésos procedimientos
¡Muchísimas gracias por el comentario Óscar!
x^3-x^2-4=0 no tiene soluciones?
Sí que tiene soluciones, pero la única solución real es x=2, las otras dos soluciones son números complejos.
3.(a+6)=27
Hola Lucas, se trata de una ecuación de primer grado, así que para resolverla simplemente debes hacer las operaciones y despejar la incógnita:
Hola buenas. Necesito tu ayuda. La función
f(x)= -x^3 -2x^2 +9x -18 que raíces tiene ? Porque no puedo sacarla por ruffini.
Hola María,
La única raíz real de esta función cúbica es x=-4,72. Lógicamente, no te salía con Ruffini porque no es un número entero, para encontrarla debes utilizar métodos más avanzados.
Tengo una ecuación que no consigo resolver por Ruffini, no sé si está mal planteada, es esta:
80X^3 – 21X^2 – 33X – 45 = 0
Me podéis ayudar?
Gracias
Hola Elvira, no la tenías mal planteada, esta ecuación no la podrás resolver por Ruffini porque no tiene ninguna solución entera.
La única solución real de la ecuación es x=1,1 por tanto no te saldrá mediante la regla de Ruffin.
Me puedes ayudar con esta
3,5,15,375,1875
Claro Evelyn, ¿pero podrías escribir bien la ecuación con su variable y sus exponentes por favor? No entiendo cómo es la ecuación.
hola quisiera resolver esta ecuación , saber que regla utiliza y como sería el paso a paso. Gracias
100 . x^3 – 28,054 x^2 + 1,36 x – 0,0492 = 0
Hola Noe,
La ecuación cúbica que propones no tiene ninguna solución entera, la única solución real de la ecuación es x=0,23.
4x^3+16x^2-45x+23 no puedo por ruffini
Hola Bryan,
No puedes solucionar la ecuación con la regla de Ruffini porque no tiene ninguna solución real.
Las soluciones de la ecuación son x=0,75, x=1,28 y x=-6,03.
Hola, me podrías ayudar con esta ecuación no sé resolverla.
×^4-6×^3+4^2+25×-30=0
Hola Paula,
Se trata de una ecuación de cuarto grado, por lo que primero debes aplicar la regla de Ruffini dos veces y hallarás las raíces
y 
Luego tienes que resolver la ecuación de segundo grado obtenida del método de Ruffini para calcular las otras dos soluciones de la ecuación, que son
y 
Hola, buenas tardes me podría de favor decir cuales son las raíces de esta ecuación?
x3-x2+x
gracias
Hola Alex,
La ecuación cúbica que propones solo tiene una raíz real, que es x=0. Las otras dos raíces son imaginarias.
(3×3+13×2-13x+2):(x-1)=
Hola Alexis,
Para resolver esta división tienes que usar la regla de Ruffini. Puedes ver cómo se hace en nuestra página hermana polinomios.org.[/latex]
Hola, buenas tardes , me gustaría saber simplemente por curiosidad y porque me gustan mucho las matemáticas cuál sería la fórmula de una ecuación de tercer y cuarto grado porque me dijeron que hay pero no las encuentro. Me serviría mucho ya que me gustaría probar que tan difíciles son
Hola Alejandro,
Hay algunas fórmulas para resolver tanto la ecuación cúbica como la ecuación cuártica, en realidad no es que sean difíciles, sino que se tarda tanto en hacer el cálculo que normalmente es más rápido con Ruffini. Además, las fórmulas que no sirven para resolver todos los casos, sino que solamente se pueden utilizar en algunas ocasiones.
Por lo tanto, sí que existen fórmulas para la ecuación de tercer grado y la de cuarto grado pero ni se pueden utilizar siempre ni es convenientes usarlas.
Hola! necesito ayuda con un ejercicio, llevo rato tratando y nada! 🙁 es parte de otro ejercicio para una exposición de mañana y no logro resolverla por mas que trate! ayuda porfa- el ejercicio es:
x^3+6x^2-13x+3=0
Buenas Loon.a,
Seguramente no puedas resolver esta ecuación cúbica porque no tiene ninguna solución real. Se debería aplicar un método más avanzado para solucionarla.
Por si te interesa, sus soluciones son x=0,26, x=1,47 y x=-7,73.
Dejen un link de referencia para poder citarlos caposss, gracias por la info!!!
Hola Jesús, debes copiar la URL que aparece en la barra de arriba de tu navegador. 🙂
hola una pregunta como se puede solucionar esta -2x^2-y+2=0 funcion cubica
Hola Carlos,
En primer lugar, se trata de una función de segundo grado, no una función cúbica, porque el grado máximo de sus términos es 2.
Aún así, esta ecuación cuadrática tiene dos incógnitas, por lo que no podrás hallar un valor concreto, solo puedes despejar una incógnita y dejarla en función de la otra. Para solucionar esta ecuación necesitas otra ecuación, de esta forma tendrás un sistema de dos ecuaciones con dos incógnitas y ya lo podrás resolver.
Puedo resolver una ecuación de tercer grado con números grandes con Ruffini? Mi docente hace que hagamos el método de Newton Raphson y se me hace muy complicado
Hola Mariana,
Sí que puedes, simplemente debes encontrar una raíz de la ecuación, tal y como se explica en este post. Sin embargo, si las raíces de la ecuación son muy grandes, te resultará muy laborioso determinar una raíz y, por tanto, puede ser que pierdas mucho tiempo en solucionar la ecuación cúbica.