En esta página encontrarás qué es un sistema compatible indeterminado. También te explicamos cuándo un sistema es compatible indeterminado y, además, podrás ver un ejemplo donde te mostramos las distintas maneras que existen para identificar este tipo de sistema.
Índice
¿Qué es un sistema compatible indeterminado?
Un sistema compatible indeterminado es un sistema de ecuaciones que tiene infinitas soluciones. Esto significa que las ecuaciones de un sistema compatible indeterminado se cumplen por cualquier valor que tomen las incógnitas.
Así pues, los sistemas de ecuaciones se pueden clasificar en tres tipos según el número de soluciones que tengan: un sistema compatible determinado (SCD) tiene una única solución, un sistema compatible indeterminado (SCI) tiene infinitas soluciones, y un sistema incompatible (SI) no tiene ninguna solución.
¿Cuándo un sistema es compatible indeterminado?
Visto el significado de un sistema de ecuaciones compatible indeterminado, vamos a estudiar cómo se puede saber si un sistema es compatible indeterminado o no.
Un sistema de ecuaciones es compatible indeterminado cuando se cumple alguna de las siguientes condiciones:
- La representación gráfica de las ecuaciones del sistema corresponde a dos rectas coincidentes, es decir, una recta está encima de la otra.
- Al intentar resolver numéricamente el sistema se obtiene una ecuación que tiene infinitas soluciones.
- Todos los coeficientes de las ecuaciones son proporcionales entre sí.
Aunque puede parecer difícil, identificar cuándo un sistema es compatible indeterminado es relativamente sencillo. A continuación, hemos resuelto un ejemplo para que veas claramente cómo se hace.
Ejemplo de sistema compatible indeterminado
En este apartado resolveremos un ejemplo de un sistema de ecuaciones lineales compatible indeterminado para que puedas entender mejor el concepto:
![\left. \begin{array}{l} 3x-2y=8 \\[2ex] 6x-4y=16 \end{array} \right\}](https://www.ejerciciosecuaciones.com/wp-content/ql-cache/quicklatex.com-6dfb9d66b988ae9eec47c91ef42e4168_l3.svg "Rendered by QuickLaTeX.com")
Primero de todo, podemos averiguar si se trata de un sistema compatible indeterminado analizando la proporcionalidad entre los coeficientes de las variables y los términos independientes:
Como podemos comprobar, todos los coeficientes de las dos ecuaciones son proporcionales entre sí, por lo que efectivamente consiste en un sistema compatible indeterminado.
Por otro lado, también podemos determinar qué tipo de sistema es intentando resolver el sistema matemáticamente. Esto se puede hacer con alguno de los siguientes cuatro métodos: método de sustitución, de reducción, de igualación o gráfico. En este ejercicio utilizaremos el método de reducción ya que las dos ecuaciones son proporcionales.
Para aplicar el método de reducción, primero multiplicamos la primera ecuación por -2:
Y luego sumamos las dos ecuaciones del sistema:
![\begin{array}{r} -6x+4y =-16 \\[1.2ex] 6x-4y = \phantom{-}16 \\ \hline \vphantom{\sqrt{x^2}} 0 = \phantom{-1}0 \end{array}](https://www.ejerciciosecuaciones.com/wp-content/ql-cache/quicklatex.com-3a3ee0102721cd8247f59ecec24a5ad7_l3.svg "Rendered by QuickLaTeX.com")
Sin embargo, obtenemos una igualdad en la que no aparece ninguna incógnita, por lo tanto, siempre se cumplirá por cualquier valor que tomen las variables. De forma que el sistema de ecuaciones lineales tiene infinitas soluciones y, en consecuencia, corresponde a un sistema compatible indeterminado.
Por último, también se puede analizar la compatibilidad del sistema representando gráficamente las dos ecuaciones:
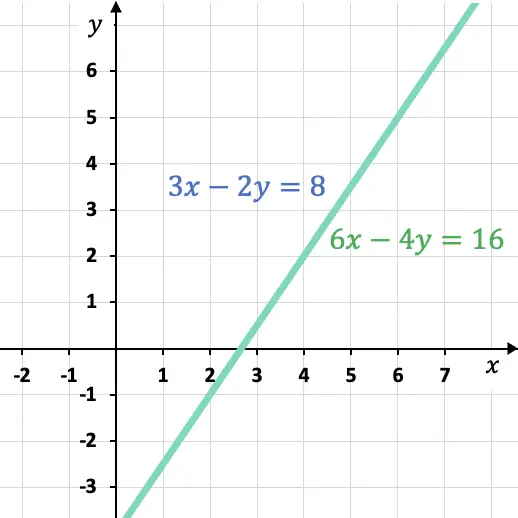
Las rectas de las dos ecuaciones son coincidentes, lo que implica que consiste en un sistema compatible indeterminado. Asimismo, las posibles soluciones del sistema son todos aquellos puntos que pertenecen a la recta del gráfico.
Sistemas compatibles indeterminados de 3 o más incógnitas
Acabamos de estudiar cómo son los sistemas compatibles indeterminados con dos ecuaciones y dos incógnitas. Pero, obviamente, un sistema también puede tener aún más ecuaciones y más incógnitas. A continuación te introduciremos un teorema que se utiliza para comprobar si un sistema con más de 2 incógnitas es compatible indeterminado o no.
El teorema de Rouché-Frobenius es muy útil para analizar la compatibilidad (o incompatibilidad) de sistemas de grandes dimensiones, se trata de un teorema que sirve para clasificar a todos los tipos de sistemas de ecuaciones calculando el rango de las matrices formadas por sus coeficientes. Y, de hecho, una vez se ha aplicado este teorema, se puede llegar a una posible solución mediante la regla de Cramer o el método de Gauss. Pero para para poder emplear todos estos métodos es necesario un conocimiento de matemáticas más avanzado.
👉👉👉 Si estás más interesad@ en este tema, te recomendamos que visites la página www.matricesydeterminantes.com, donde se explica paso a paso todos los métodos que existen para solucionar un sistema de ecuaciones con 3 (o más) incógnitas.👈👈👈
