Sistema compatible

En esta página te explicaremos qué es un sistema compatible. Además, te enseñaremos los 2 tipos de sistemas de ecuaciones compatibles que existen (SCD y SCI) y podrás ver ejemplos de cada uno. Asimismo, encontrarás cuál es la diferencia entre un sistema compatible y un sistema incompatible. Y, finalmente, te mostraremos un método para identificar sistemas compatibles de 3 (o más incógnitas).

¿Qué es un sistema compatible?

Un sistema compatible es un sistema de ecuaciones que tiene solución, es decir, que se puede resolver. Cuando el sistema tiene una única solución es un sistema compatible determinado (SCD), en cambio, cuando el sistema tiene infinitas soluciones es un sistema compatible indeterminado (SCI).

Sistema compatible determinado

Como hemos visto en la definición de sistema compatible, un sistema de ecuaciones compatible determinado es aquel que posee una sola solución.

Por lo tanto, para identificar este tipo de sistema compatible basta con intentar resolverlo, y si el sistema tiene 1 solución significa que es compatible determinado.

Veamos un ejemplo para acabarlo de entender:

Para determinar el sistema de ecuaciones debemos utilizar alguno de los cuatro métodos posibles: método de sustitución, de reducción, de igualación o gráfico. En este ejercicio usaremos el método de sustitución ya que normalmente es el más fácil.

De modo que despejamos la variable y de la primera ecuación:

Sustituimos la expresión algebraica hallada en la segunda ecuación:

Ahora calculamos el valor de la incógnita x resolviendo la ecuación resultante:

Y, por último, sustituimos el valor hallado de x en la primera ecuación para así calcular el valor de la variable y:

En conclusión, el resultado del sistema de ecuaciones lineales es:

Como el sistema de ecuaciones tiene una única solución, se trata de un sistema compatible determinado.

Asimismo, se puede demostrar la compatibilidad del sistema representando gráficamente sus dos ecuaciones:

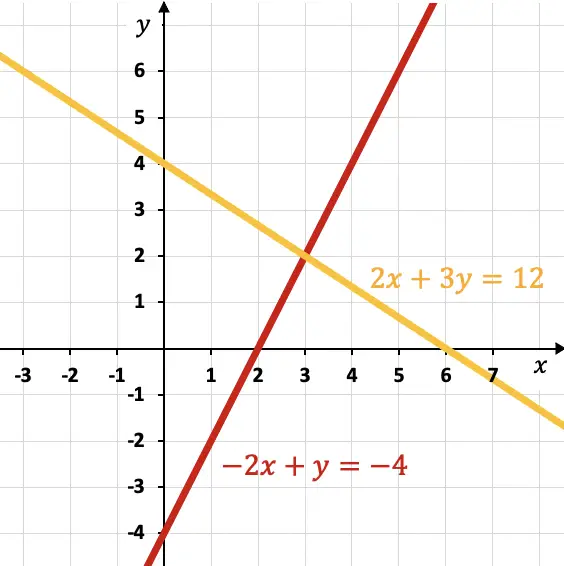
Cuando las dos ecuaciones representadas en el gráfico se cortan, quiere decir que consiste en un sistema compatible determinado. Además, las dos rectas siempre se intersecan justo en la solución del sistema de ecuaciones, que en este caso es el punto (3,2).

Una vez has visto cómo se resuelve un sistema de ecuaciones compatible determinado, ahora puedes practicar hacer problemas de sistemas de ecuaciones con dos incógnitas.

Sistema compatible indeterminado

Una vez ya sabemos cómo se resuelven los sistemas compatibles determinados, vamos a ver cómo son los sistemas compatibles indeterminados.

Un sistema compatible indeterminado posee infinitas soluciones, de manera que sabremos que tenemos este tipo de sistema cuando al intentar solucionarlo nos encontramos con una ecuación que también tiene infinitas soluciones.

Para comprender mejor el concepto, vamos a resolver un ejemplo de sistema de ecuaciones lineales compatible indeterminado:

Como hemos visto antes, un sistema de ecuaciones se puede calcular mediante el método de sustitución, de reducción, de igualación o gráfico. En este problema aplicaremos el método de reducción porque las dos ecuaciones son proporcionales.

Entonces, primero multiplicamos la primera ecuación por -2:

Y después sumamos las dos ecuaciones del sistema:

Sin embargo, hemos obtenido una igualdad en la que no aparece ninguna incógnita, lo que significa que siempre se cumplirá por cualquier valor que tomen las variables. De forma que el sistema de ecuaciones lineales tiene infinitas soluciones y, en consecuencia, corresponde a un sistema compatible indeterminado.

Finalmente, también se puede analizar la compatibilidad del sistema representando gráficamente las dos ecuaciones:

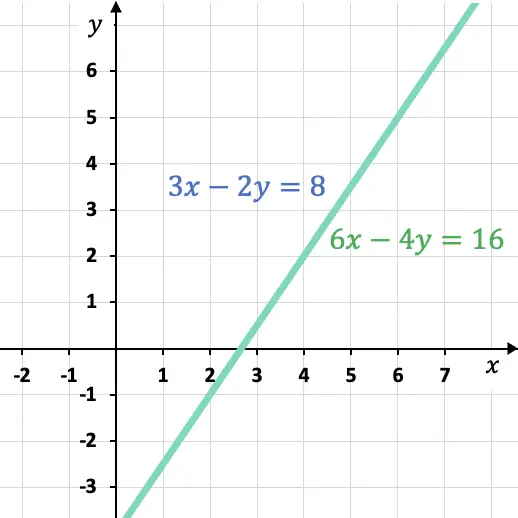
Las rectas de las dos ecuaciones son coincidentes, por lo que se trata de un sistema compatible indeterminado. Asimismo, las posibles soluciones del sistema son todos aquellos puntos que pertenecen a la recta del gráfico.

¿Cuándo un sistema es compatible y cuándo incompatible?

Como hemos visto, los sistemas de ecuaciones compatibles pueden clasificarse en dos tipos: sistemas compatibles determinados (SCD) y sistemas compatibles indeterminados (SCI). Pero debes saber que aún existe otro tipo de sistema, llamado sistema incompatible (SI).

Un sistema incompatible (SI) es un sistema de ecuaciones que no tiene solución. Por lo tanto, la diferencia entre los sistemas compatibles y los incompatibles radica en el número de soluciones del sistema: cuando el sistema tiene solución (ya sea una única o infinitas) es compatible, en cambio, cuando el sistema no tiene ninguna solución es incompatible.

Entender qué es un sistema incompatible es relativamente fácil. Sin embargo, identificar cuándo un sistema es incompatible es bastante más complicado, puedes ver cómo se hace en este ejemplo de sistema incompatible.

Sistemas compatibles de 3 o más incógnitas

Acabamos de analizar matemáticamente cómo son los sistemas compatibles con dos ecuaciones y dos incógnitas, ya sean SCD o SCI. No obstante, un sistema puede esta formado por más ecuaciones y más incógnitas. En este apartado te introduciremos un método que se utiliza para hallar si un sistema con más de 2 variables es compatible o no.

El método más empleado para determinar la compatibilidad (o incompatibilidad) de sistemas de grandes dimensiones es el teorema de Rouché-Frobenius, un teorema que sirve para clasificar a todos los tipos de sistemas de ecuaciones calculando el rango de las matrices formadas por sus coeficientes. Sin embargo, para poder aplicar este teorema se necesita tener un conocimiento de matemáticas más avanzado.

👉👉👉 Si estás más interesad@ en este tema, te recomendamos que visites la página www.matricesydeterminantes.com, donde se explica paso a paso este teorema y, además, podrás ver otros métodos para solucionar sistemas de ecuaciones con 3 (o más) incógnitas.👈👈👈