▷ Discriminante de una ecuación de segundo grado

Aquí encontrarás qué es el discriminante de una ecuación de segundo grado y cómo se calcula. Además, explicamos cómo se pueden saber las soluciones que tiene una ecuación de segundo grado con el valor del discriminante (positivo, negativo o nulo). Finalmente, podrás practicar con ejercicios resueltos paso a paso.

Índice

¿Qué es el discriminante de una ecuación de segundo grado?

El discriminante de una ecuación de segundo grado es un cálculo que permite saber el número de soluciones que tiene dicha ecuación. En concreto, el discriminante de una ecuación de segundo grado es igual a la expresión de dentro de la raíz cuadrada de su fórmula, esto es, Δ=b²-4ac.

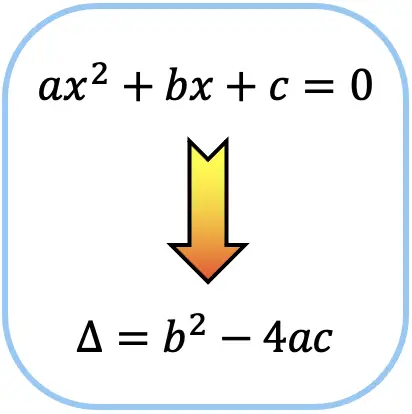
discriminante de una ecuacion de segundo grado

Normalmente, en álgebra se representa el discriminante de una ecuación de segundo grado (o cuadrática) mediante la letra griega delta mayúscula Δ, pero también se puede hacer con la letra D.

Ejemplo de cómo calcular el discriminante de una ecuación de segundo grado

Una vez hemos visto cuál es la definición del discriminante, vamos a ver cómo se resuelve mediante un ejemplo:

$x^2+5x+4 = 0$

La fórmula del discriminante de una ecuación de segundo grado es la siguiente:

$\Delta = b^2-4ac$

Por lo tanto, para hallar el discriminante simplemente tenemos que sustituir las variables de la fórmula por sus valores correspondientes: $a$ es el coeficiente del término cuadrático que en este caso es 1, $b$ es el término que acompaña al término de primer grado que es 5, y $c$ es el término independiente, es decir, 4.

$\begin{aligned} \Delta & = 5^2-4\cdot 1\cdot 4 \\[1.5ex] & = 25 -16 \\[1.5ex] & = \bm{9} \end{aligned}$

¿Qué significa el discriminante de una ecuación de segundo grado?

El significado del discriminante de una ecuación de segundo grado es muy importante, ya que se utiliza para saber el número de soluciones (o raíces) que tiene la ecuación cuadrática.

Si el discriminante es positivo (Δ>0) significa que la ecuación de segundo grado tiene dos soluciones distintas.
Si el discriminante es nulo (Δ=0) quiere decir que la ecuación de segundo grado tiene dos soluciones iguales.
Si el discriminante es negativo (Δ<0) implica que la ecuación de segundo grado no tiene ninguna solución real.

Por otro lado, aunque el valor del discriminante sirve para determinar el número de soluciones de la ecuación cuadrática, debes tener en cuenta que no se pueden hallar dichas soluciones a través del discriminante, sino que se debe resolver la ecuación mediante su fórmula.

Aunque parezca extraño, estas reglas matemáticas siempre se cumplen independientemente de cómo sea la ecuación de grado 2. A continuación, veremos por qué el discriminante indica las soluciones de una ecuación de segundo grado.

Discriminante positivo

Como hemos visto arriba, cuando el discriminante es mayor que cero la ecuación tiene dos soluciones reales diferentes. Esto es debido a que en la fórmula de la ecuación de segundo grado obtenemos dos valores distintos (el positivo y el negativo) a partir de la raíz cuadrada.

$\displaystyle x=\cfrac{-b \pm \sqrt{\Delta}}{2a} \ \xrightarrow{\Delta \ > \ 0} \ \begin{cases} x=\cfrac{-b + \sqrt{\Delta}}{2a} \\[4ex] x=\cfrac{-b - \sqrt{\Delta}}{2a} \end{cases}$

Discriminante nulo

Cuando el discriminante es igual a cero la ecuación de segundo grado tiene 2 soluciones equivalentes, ya que la raíz cuadrada queda anulada en la fórmula y, en consecuencia, solo se obtiene un valor de la fórmula.

$\displaystyle x=\cfrac{-b \pm \sqrt{\Delta}}{2a} \ \xrightarrow{\Delta \ = \ 0} \ x=\cfrac{-b \pm \sqrt{0}}{2a}= \cfrac{-b}{2a}$

Sin embargo, aunque solamente se consiga un valor de la fórmula no significa que la ecuación tenga una única solución, sino que la ecuación tiene dos soluciones repetidas, o dicho de otra forma, tiene una solución doble.

Discriminante negativo

Cuando el discriminante es menor que cero la ecuación de segundo grado no tiene ninguna solución real, ya que no existen la raíces cuadradas de números negativos:

$\displaystyle x=\cfrac{-b \pm \sqrt{\Delta}}{2a} \ \xrightarrow{\Delta \ < \ 0} \ \color{red} \bm{\times}$

En realidad, sí que se podría solucionar la ecuación cuadrática, pero sus dos soluciones son complejas (o imaginarias) y para entenderlas se necesita un conocimiento de matemáticas más avanzado.

Ejercicios resueltos del discriminante de una ecuación de segundo grado

Ejercicio 1

Calcula el discriminante de la siguiente ecuación de segundo grado y determina cuántas soluciones tiene:

$x^2-3x-2 = 0$

Ver solución

La fórmula del discriminante de una ecuación de segundo grado es:

$\Delta = b^2-4ac$

De manera que solamente debemos sustituir los valores de la ecuación en la fórmula, que son $a=1, b=-3$ y $c=-2.$

$\begin{aligned} \Delta & = (-3)^2-4\cdot 1\cdot (-2) \\[1.5ex] & = 9+8 \\[1.5ex] & = \bm{17} \end{aligned}$

El discriminante es positivo, así que la ecuación de segundo grado tiene dos soluciones distintas.

Ejercicio 2

Halla el discriminante de la siguiente ecuación cuadrática y averigua cuántas soluciones tiene:

$6x+3x^2+3 = 0$

Ver solución

La fórmula del discriminante de la ecuación cuadrática es:

$\Delta = b^2-4ac$

Por tanto, tenemos que sustituir los coeficientes de la ecuación en la fórmula. Sin embargo, en este caso la ecuación está desordenada así que nos tenemos que fijar bien: $a$ es el coeficiente del término cuadrático, es decir 3; $b$ es el coeficiente del término de primer grado, o sea 6; y por último $c$ es el término sin incógnita, esto es 3.

$\begin{aligned} \Delta & = 6^2-4\cdot 3\cdot 3 \\[1.5ex] & = 36-36 \\[1.5ex] & = \bm{0} \end{aligned}$

El discriminante es igual a 0, por lo que la ecuación de segundo grado tiene dos soluciones iguales..

Ejercicio 3

Encuentra el discriminante de la siguiente ecuación de segundo grado y razona cuántas soluciones tiene:

$3x^2-2x+5 = 0$

Ver solución

El discriminante de una ecuación de segundo grado se calcula con la siguiente fórmula:

$\Delta = b^2-4ac$

De forma que debemos cambiar las variables de la ecuación de la fórmula por sus valores, que son $a=3, b=-2$ y $c=5.$

$\begin{aligned} \Delta & = (-2)^2-4\cdot 3\cdot 5 \\[1.5ex] & = 4-60 \\[1.5ex] & = \bm{-54} \end{aligned}$

El valor del discriminante es negativo, con lo que la ecuación cuadrática no tiene ninguna solución real.

Ejercicio 4

Determina el discriminante de la siguiente ecuación de cuadrática y el número de soluciones que tiene:

$x^2+6 = 0$

Ver solución

Aplicamos la fórmula del discriminante de una ecuación de segundo grado:

$\Delta = b^2-4ac$

Pero en este problema no hay término de grado 1, por lo tanto, los valores de las letras son $a=1, b=0$ y $c=6.$

$\begin{aligned} \Delta & = 0^2-4\cdot 1\cdot 6 \\[1.5ex] & = 0-24 \\[1.5ex] & = \bm{-24} \end{aligned}$

El discriminante es negativo, así que no existe ninguna solución real de la ecuación de segundo grado.

Ejercicio 5

Calcula el valor de $k$ para que la siguiente ecuación tenga dos soluciones idénticas:

$kx^2+10x- 5=0$

Ver solución

Para que la ecuación de segundo grado tenga 2 soluciones iguales, el discriminante debe dar como resultado 0. Por lo tanto, primero intentamos calcular el discriminante con su fórmula:

$\begin{aligned}\Delta & = b^2-4ac \\[1.5ex] & = 10^2-4\cdot k\cdot (-5) \\[1.5ex] & = 100+20k \end{aligned}$

Y ahora igualamos la expresión algebraica obtenida a cero y resolvemos la ecuación resultante:

$100+20k=0$

$20k=-100$

$k=\cfrac{-100}{20}$

$k=-5$

En conclusión, para que se cumpla la condición del enunciado del problema $k$ debe valer -5.

Otros tipos de discriminantes

Acabamos de analizar cuál es el discriminante de una ecuación de segundo grado y cómo se determina. Sin embargo, también se puede hallar el discriminante de otros tipos de ecuaciones o funciones. Y todos ellos se representan mediante el símbolo Δ.

Por ejemplo, se puede sacar el discriminante de una ecuación de tercer grado usando la siguiente la siguiente fórmula:

$ax^3+bx^2+cx+d = 0$

$\Delta = b^2c^2-4ac^3-4b^3d-27a^2d^2+18abcd$

El discriminante solo permite identificar el número de soluciones de la ecuación, pero para averiguar el valor de dichas soluciones se debe hacer un procedimiento complicado. Aquí puedes ver cómo resolver ecuaciones de tercer grado paso a paso.

Asimismo, es posible resolver el discriminante de una sección cónica (una función de segundo grado con dos incógnitas) utilizando la siguiente fórmula:

$ax^2 + bxy + cy^2 + dx + ey + f= 0$

$\Delta = b^2-4ac$

Este discriminante permite identificar la forma de la sección cónica en cuestión: si el discriminante es positivo la ecuación describe una elipse o una circunferencia, si es nulo una parábola, y si es negativo una hipérbola.

De hecho, se puede hallar el discriminante de cualquier polinomio en general, pero para ello es necesario tener un nivel de matemáticas muy avanzado.

También te puede interesar:

¿Qué es el discriminante de una ecuación de segundo grado?

Ejemplo de cómo calcular el discriminante de una ecuación de segundo grado

¿Qué significa el discriminante de una ecuación de segundo grado?

Discriminante positivo

Discriminante nulo

Discriminante negativo

Ejercicios resueltos del discriminante de una ecuación de segundo grado

Ejercicio 1

Ejercicio 2

Ejercicio 3

Ejercicio 4

Ejercicio 5

Otros tipos de discriminantes

Deja un comentario Cancelar respuesta